案例6:使用Simulink生成传动系统故障数据
本案例将展示,如何使用Simulink模型生成故障和健康数据。随后,生成的故障和健康数据将被用来开发状态监控算法。本案例聚焦于传动系统,将模拟齿轮齿故障、传感器漂移故障和轴磨损故障
第一步:传动系统模型
变速箱体模型使用Simscape中的传动系统模块(需安装Simscape Driveline)来模拟简单的传动系统。传动系统包括转矩驱动器、传动轴、离合器和连接到输出轴的高低齿轮
下面直接导入Matlab中已有的变速箱体模型
传动系统中包含了一个振动传感器,用来监控箱体振动。箱体模型将轴的角位移转化为箱体上的线性位移。将箱体建模为质量弹簧阻尼系统和从箱体上测得的振动(箱体加速度)
下面可在Simulink中打开箱体模型
第二步:故障建模
传动系统包含了诸如振动传感器漂移、齿轮齿故障和轴磨损故障。传感器漂移可以很容易地通过在传感器模型中加上偏移量模拟。该偏移量是通过模型变量SDrift控制,当 SDrift为0时代表无传感器故障
轴磨损故障通过变量子系统模拟。在这种情况下,子系统变量改变轴阻尼,但变量子系统可以用来完全改变轴模型的实现。所选择的变量通过模型变量ShaftWear控制,当ShaftWear为0时,表示无轴磨损故障
齿轮齿故障通过在传动轴转动的固定位置引入扰动力矩实现。轴位置使用弧度测得,当轴位置为在0附近的小窗范围内时,将扰动力施加于轴上。扰动大小通过模型变量ToothFaultGain控制,当ToothFaultGain为0时,表示无齿轮齿故障
第三步:模拟故障和健康数据
通过控制并调节传感器漂移、齿轮齿故障、轴磨损三种故障类型出现及严重程度的变量配置传动模型。通过改变模型变量,SDrift,ToothFaultGain,ShaftWear三个变量,可以模拟出不同故障类型下的数据。使用Simulink.SimulationInput对象中的数组,可以定义不同的模拟场景。例如,为每个模型变量分配一个数组,然后使用ndgrid函数为每组模型变量的组合生成一个Simulink.SimulationInput对象
toothFaultArray = -2:2/10:0; % 齿轮故障增益值
sensorDriftArray = -1:0.5:1; % 传感器漂移偏移值
shaftWearArray = [0 -1]; % 对应驱动轴磨损不同的变量值
% 创建组合所有值的n-维数组
[toothFaultValues,sensorDriftValues,shaftWearValues] = ...
ndgrid(toothFaultArray,sensorDriftArray,shaftWearArray);
for ct = numel(toothFaultValues):-1:1
% 对每个模型参数输入的组合生成一个Simulink.SimulationInput结果
siminput = Simulink.SimulationInput(mdl);
% 修改模型参数
siminput = setVariable(siminput,'ToothFaultGain',toothFaultValues(ct));
siminput = setVariable(siminput,'SDrift',sensorDriftValues(ct));
siminput = setVariable(siminput,'ShaftWear',shaftWearValues(ct));
% 收集数组中的模拟输入
gridSimulationInput(ct) = siminput;
end相似的,创建每种随机模型变量值的组合。同时确保包含0值,以使得只包含三种故障模式的子集对应的变量组合存在
rng('default'); % 设置随机种子
toothFaultArray = [0 -rand(1,6)]; % 齿轮故障增益值
sensorDriftArray = [0 randn(1,6)/8]; % 传感器漂移偏移值
shaftWearArray = [0 -1]; % 对应驱动轴磨损不同的变量值
%创建组合所有值的n-维数组
[toothFaultValues,sensorDriftValues,shaftWearValues] = ...
ndgrid(toothFaultArray,sensorDriftArray,shaftWearArray);
for ct=numel(toothFaultValues):-1:1
% 对每个模型参数输入的组合生成一个Simulink.SimulationInput结果
siminput = Simulink.SimulationInput(mdl);
% 修改模型参数
siminput = setVariable(siminput,'ToothFaultGain',toothFaultValues(ct));
siminput = setVariable(siminput,'SDrift',sensorDriftValues(ct));
siminput = setVariable(siminput,'ShaftWear',shaftWearValues(ct));
% 收集数组中的模拟输入
randomSimulationInput(ct) = siminput;
end在Simulink.SimulationInput数组对象被定义后,使用generateSimulationEnsemble函数运行这些模拟过程。generateSimulationEnsemble函数对模型进行配置,将记录的数据保存到文件中,对信号记录使用时间表标准化,并存储Simulink.SimulationInput对象到存储文件中。generateSimulationEnsemble函数返回状态标志,反映模拟过程是否成功运行完成
以上代码从网格化的变量值中创造了110组模拟输入,98组来自随机变量值的模拟输入输出了总共208次模拟。在标准桌面算力中并行运行这208次模拟过程需耗时大约10分钟,生成大于10GB数据。方便起见,可以选择只运行其中的10次模拟过程(作者注:本文件夹中包含了所有的208次模拟数据,可直接加载,不必再次运行)
% 运行模拟过程,并创造集成数据以管理模拟结果
if ~exist(fullfile(pwd,'Data'),'dir')
mkdir(fullfile(pwd,'Data')) % 当前目录下,创建存储数据的Data文件夹
end
runAll = true;
if runAll %并行运行所有模拟,需要parallel computing工具箱
[ok,e] = generateSimulationEnsemble([gridSimulationInput, randomSimulationInput], ...
fullfile(pwd,'Data'),'UseParallel', true);
else %运行前10次模拟
[ok,e] = generateSimulationEnsemble(gridSimulationInput(1:10), fullfile(pwd,'Data')); %#ok<*UNRCH>
end[18-Feb-2020 23:40:27] Checking for availability of parallel pool… Starting parallel pool (parpool) using the ‘local’ profile … Connected to the parallel pool (number of workers: 4). [18-Feb-2020 23:41:27] Starting Simulink on parallel workers… [18-Feb-2020 23:41:45] Configuring simulation cache folder on parallel workers… [18-Feb-2020 23:41:48] Loading model on parallel workers… [18-Feb-2020 23:41:56] Transferring base workspace variables used in the model to parallel workers… [18-Feb-2020 23:42:17] Running simulations… Analyzing and transferring files to the workers …done. [18-Feb-2020 23:44:45] Completed 1 of 208 simulation runs [18-Feb-2020 23:44:46] Completed 2 of 208 simulation runs [18-Feb-2020 23:44:47] Completed 3 of 208 simulation runs … [19-Feb-2020 01:12:21] Completed 207 of 208 simulation runs [19-Feb-2020 01:12:30] Completed 208 of 208 simulation runs [19-Feb-2020 01:12:33] Cleaning up parallel workers…
generateSimulationEnsemble函数运行并保存模拟结果,可使用simulationEnsembleDatastore命令来创建一个模拟集成模块来处理和分析模拟结果(数据已存在时,直接加载)
第四步:处理模拟结果
simulationEnsembledatastore命令生成了一个指向模拟结果的集成对象。使用这个集成对象可以准备并分析每个在集成对象元素中的数据。集成对象列出了所有的数据变量,同时在默认情况下,这些变量可读
分析时,仅读取Vibration,Tacho信号和Simulink.SimulationInput即可。Simulink.SimulationInput中保存有模型变量值,同时也可被用来创建集成对象中元素的故障标签。可以使用read命令来读取集成对象的数据元素:
从返回的数据中提取振动信号并画出它
vibration = data.Vibration{1};
plot(vibration.Time,vibration.Data)
title('Vibration')
ylabel('Acceleration')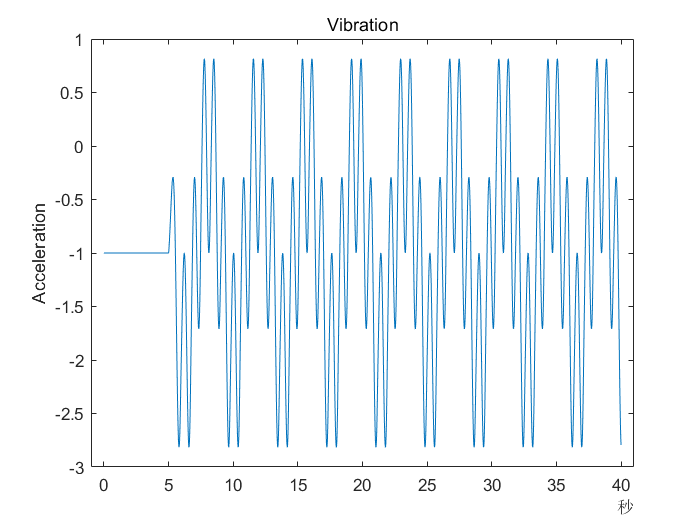
前10秒数据中包含了传动系统起步阶段,因此分析时需去除这部分数据
idx = vibration.Time >= seconds(10);
vibration = vibration(idx,:);
vibration.Time = vibration.Time - vibration.Time(1);Tacho转速信号中包含了驱动轴和负载轴旋转的脉冲,但分析时,尤其是当时间同步平均时,需要轴旋转的次数。以下代码去除了转速信号的前10秒,并且在tachoPulses中找出轴旋转次数
tacho = data.Tacho{1};
idx = tacho.Time >= seconds(10);
tacho = tacho(idx,:);
plot(tacho.Time,tacho.Data)
title('Tacho pulses')
legend('Drive shaft','Load shaft') % 负载轴转得比驱动轴更慢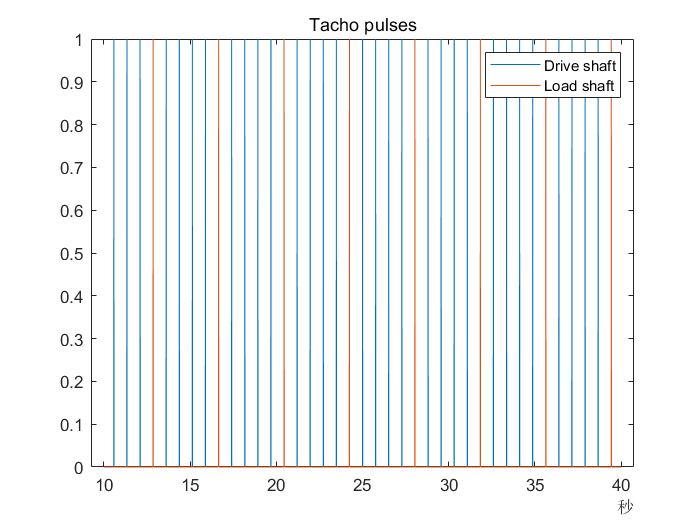
Simulink.SimulationInput.Variables属性中包含了模拟用的故障参数值,这些值可以被用来对每个集成对象元素创建故障标签
vars = data.SimulationInput{1}.Variables;
idx = strcmp({vars.Name},'SDrift');
if any(idx)
sF = abs(vars(idx).Value) > 0.01; % 微小偏移值不算故障
else
sF = false;
end
idx = strcmp({vars.Name},'ShaftWear');
if any(idx)
sV = vars(idx).Value < 0;
else
sV = false;
end
if any(idx)
idx = strcmp({vars.Name},'ToothFaultGain');
sT = abs(vars(idx).Value) < 0.1; % 微小齿轮齿故障值不算故障
else
sT = false
end
faultCode = sF + 2*sV + 4*sT; % 表征不同故障类型的故障码处理后的振动和转速信号以及故障标签被加到集成对象中,以便之后使用
sdata = table({vibration},{tachoPulses},sF,sV,sT,faultCode, ...
'VariableNames',{'Vibration','TachoPulses','SensorDrift','ShaftWear','ToothFault','FaultCode'}) 集成对象的ConditionVariables属性可以被用来识别集成对象中的变量,包含状态和故障标签数据。设定包含新创建的故障标签属性
上述代码被用来处理集成对象中的单个元素。要处理对象中所有的元素,须将以上代码转成prepareData方法,并且使用集成对象hasdata命令进行循环,将同样的操作应用于集成对象中的所有元素中。集成对象中元素可以用过将集成对象分块划分,并将划分的部分并行处理即可实现整体的并行化处理
prepareData方法如下:
function sData = prepareData(data)
%%
%
% Clean up the signals in the data:
% Vibration signal - remove the 1st 10 seconds of data and any duplicte times.
% Tacho - remove 1st 10 seconds, find rising edge times
%The first 10 seconds of the simulation contains data where the
%transmission system is starting up; for analysis we discard this data.
Vibration = data.Vibration{1};
plot(Vibration.Time,Vibration.Data)
title('Vibration')
idx = Vibration.Time >= seconds(10);
Vibration = Vibration(idx,:);
Vibration.Time = Vibration.Time - Vibration.Time(1);
%The tacho signal contains pulses for the rotations of the drive and load
%shafts. Later we use time synchronous averaging on the vibration data and
%that requires the times of shaft rotations, the following code discards
%the first 10 seconds of the tacho data and finds the shaft rotation times
%in TachoPulses.
Tacho = data.Tacho{1};
idx = Tacho.Time >= seconds(10);
Tacho = Tacho(idx,:);
plot(Tacho.Time,Tacho.Data)
title('Tacho pulses')
idx = diff(Tacho.Data(:,2)) > 0.5;
tachoPulses = Tacho.Time(find(idx)+1)-Tacho.Time(1);
%The Simulink.SimulationInput.Variables property contains the values of the
%fault parameters used for the simulation, these values allow us to create
%fault labels for each ensemble member.
vars = data.SimulationInput{1}.Variables;
sF = false; sV = false; sT = false;
idx = strcmp({vars.Name},'SDrift');
if any(idx)
sF = abs(vars(idx).Value) > 0.01; %Small drift values are not faults
end
idx = strcmp({vars.Name},'ShaftWear');
if any(idx)
sV = vars(idx).Value < 0;
end
idx = strcmp({vars.Name},'ToothFaultGain');
if any(idx)
sT = abs(vars(idx).Value) < 0.1; %Small tooth fault values are not faults
end
FaultCode = sF+2*sV+4*sT; %A fault code to capture different fault conditions
%Collect processed data into a table
sData = table({Vibration},{tachoPulses},sF,sV,sT,FaultCode, ...
'VariableNames',{'Vibration','TachoPulses','SensorDrift','ShaftWear','ToothFault','FaultCode'});
endreset(ens)
runLocal = false;
if runLocal
% 处理集成对象中的单个元素
while hasdata(ens)
data = read(ens);
addData = prepareData(data);
writeToLastMemberRead(ens,addData)
end
else
% 将集成对象划分成多个块,然后并行处理每个块
n = numpartitions(ens,gcp);
parfor ct = 1:n
subens = partition(ens,n,ct);
while hasdata(subens)
data = read(subens);
addData = prepareData(data);
writeToLastMemberRead(subens,addData)
end
end
end使用hasdata和read方法从集成对象元素(从208个元素中每隔10条取一条)中提取振动信号并画出
reset(ens)
ens.SelectedVariables = "Vibration";
figure,
ct = 1;
while hasdata(ens)
data = read(ens);
if mod(ct,10) == 0
vibration = data.Vibration{1};
plot(vibration.Time,vibration.Data)
hold on
end
ct = ct + 1;
end
hold off
title('Vibration signals')
ylabel('Acceleration')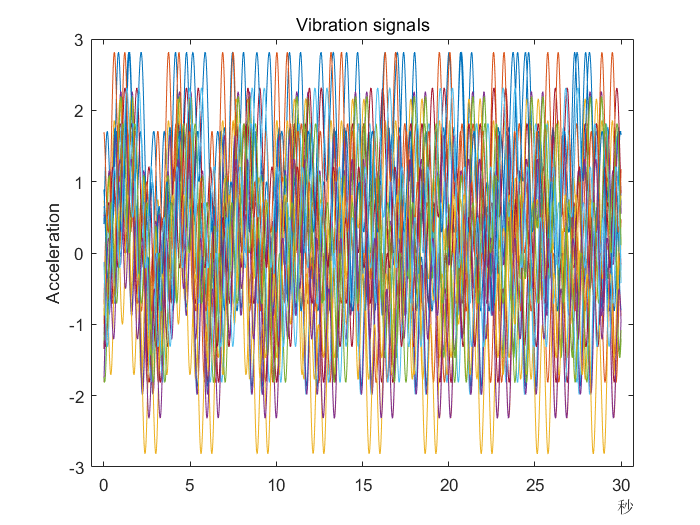
第五步:分析模拟数据
至此,数据已被清洗并预处理过,并且可以被用来提取可被用于分类不同故障类型的特征。先对集成对象进行配置,使得它只返回处理过的数据
对集成对象中的每个元素提取一些时序特征和频谱特征。它们包括诸如信号均值、方差、峰峰值,非线性信号特征诸如近似熵、李雅普诺夫指数,频谱特征诸如振动信号时间同步平均的频率峰值以及时间同步平均包络谱信号。analyzeData函数包含了完整的特征提取过程。本实例计算了时间同步平均振动信号的频谱
vibration = data.Vibration{1};
% 将振动信号插值为适合快速傅里叶变换的周期时序
np = 2^floor(log(height(vibration))/log(2));
dt = vibration.Time(end)/(np-1);
tv = 0:dt:vibration.Time(end);
y = retime(vibration,tv,'linear');
% 计算振动信号的时间同步平均
tp = seconds(data.TachoPulses{1});
vibrationTSA = tsa(y,tp);
figure
plot(vibrationTSA.ttTime,vibrationTSA.tsa)
title('Vibration time synchronous average')
ylabel('Acceleration')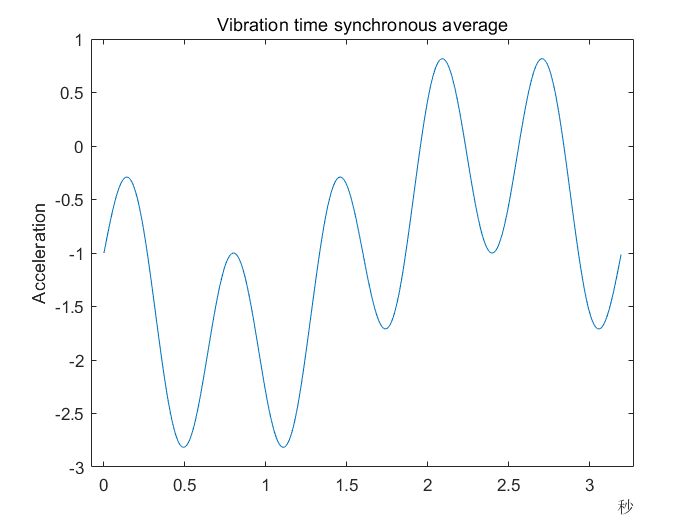
% 计算时间同步平均的频谱
np = numel(vibrationTSA);
f = fft(vibrationTSA.tsa.*hamming(np))/np;
frTSA = f(1:floor(np/2)+1); % 时间同步平均频率响应
wTSA = (0:np/2)/np*(2*pi/seconds(dt)); % 时间同步平均谱频率
mTSA = abs(frTSA); % 时间同步平均谱量级
figure
semilogx(wTSA,20*log10(mTSA))
title('Vibration spectrum')
xlabel('rad/s')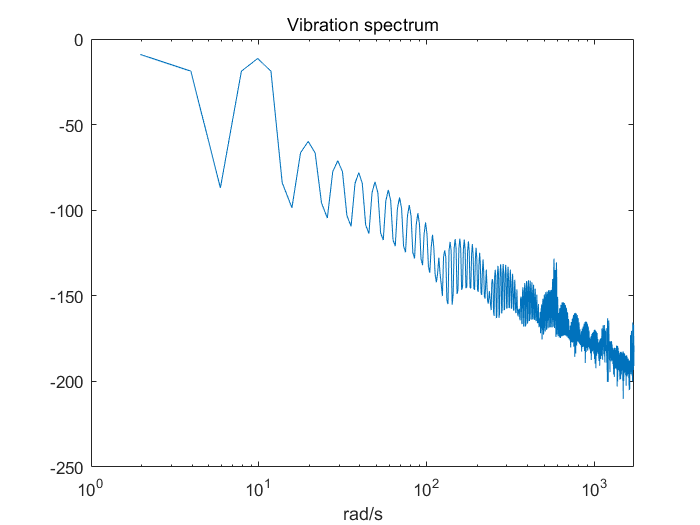
对应于峰值的频率可以作为分类不同故障类型的有用特征使用。以下代码将使用analyzeData函数对集成对象中的所有存储元素计算以上提到的所有特征(该步骤在标准桌面算力下,需耗时约30分钟,可以使用partition命令并行运算)。这些特征的名称将在调用writeToLastMemberRead函数将计算得到的特征假如到单个元素存储中之前,被加入到数据的属性中
function sData = analyzeData(data)
%%
%
% Derive features from the vibration signal. Later we use these features
% to determine the type of fault from the vibration signal as well as for
% selecting the minimum number of features needed.
%
% Copyright 2017 MathWorks Inc.
%创建将要计算的特征表
varnames = {...
'SigMean', ...
'SigMedian', ...
'SigRMS', ...
'SigVar', ...
'SigPeak', ...
'SigPeak2Peak', ...
'SigSkewness', ...
'SigKurtosis', ...
'SigCrestFactor', ...
'SigMAD', ...
'SigRangeCumSum', ...
'SigCorrDimension', ...
'SigApproxEntropy', ...
'SigLyapExponent', ...
'PeakFreq', ...
'HighFreqPower', ...
'EnvPower', ...
'PeakSpecKurtosis'};
if ischar(data)
%返回需要计算特征的名称
sData = varnames(:);
return
end
%提取被用来计算特征的振动信号
Vibration = data.Vibration{1};
%将振动信号插值为适合快速傅里叶变换的周期时序
np = 2^floor(log(height(Vibration))/log(2));
dt = Vibration.Time(end)/(np-1);
tv = 0:dt:Vibration.Time(end);
y = retime(Vibration,tv,'linear');
%信号均值
SigMean = mean(Vibration.Data);
%信号中值
SigMedian = median(Vibration.Data);
%信号均方根值
SigRMS = rms(Vibration.Data);
%信号方差
SigVar = var(Vibration.Data);
%信号峰值
SigPeak = max(Vibration.Data);
%信号峰峰值
SigPeak2Peak = peak2peak(Vibration.Data);
%信号偏度
SigSkewness = skewness(Vibration.Data);
%信号峰度
SigKurtosis = kurtosis(Vibration.Data);
%信号峰值系数
SigCrestFactor = peak2rms(Vibration.Data);
%信号中值绝对偏差
SigMAD = mad(Vibration.Data);
%信号累计和范围
d = cumsum(Vibration.Data);
SigRangeCumSum = max(d)-min(d);
%信号关联维数
SigCorrDimension = correlationDimension(y.Data);
%信号近似熵
SigApproxEntropy = approximateEntropy(y.Data);
%信号李雅普诺夫指数
SigLyapExponent = lyapunovExponent(y.Data,1/seconds(dt));
%计算时间同步平均振动信号的快速傅里叶变换
dt = seconds(dt);
tp = seconds(data.TachoPulses{1});
vibrationTSA = tsa(y,tp);
np = numel(vibrationTSA);
f = fft(vibrationTSA.tsa.*hamming(np))/np;
frTSA = f(1:floor(np/2)+1);
wTSA = (0:np/2)/np*(2*pi/dt);
mTSA = abs(frTSA);
%频率峰值
[~,idx] = max(mTSA);
PeakFreq = wTSA(idx);
%高于30Hz的功率
HighFreqPower = sum(mTSA(wTSA > 30).^2);
%时间同步平均的包络
M_env = envspectrum(vibrationTSA);
%包络谱功率
EnvPower = sum(M_env.^2);
%最大谱峭度处的频率
[~,~,~,fc] = kurtogram(y.Data,1/dt,8);
PeakSpecKurtosis = fc;
%保存计算结果值
varnames = {...
'SigMean', ...
'SigMedian', ...
'SigRMS', ...
'SigVar', ...
'SigPeak', ...
'SigPeak2Peak', ...
'SigSkewness', ...
'SigKurtosis', ...
'SigCrestFactor', ...
'SigMAD', ...
'SigRangeCumSum', ...
'SigCorrDimension', ...
'SigApproxEntropy', ...
'SigLyapExponent', ...
'PeakFreq', ...
'HighFreqPower', ...
'EnvPower', ...
'PeakSpecKurtosis'};
sData = table(...
SigMean, ...
SigMedian, ...
SigRMS, ...
SigVar, ...
SigPeak, ...
SigPeak2Peak, ...
SigSkewness, ...
SigKurtosis, ...
SigCrestFactor, ...
SigMAD, ...
SigRangeCumSum, ...
SigCorrDimension, ...
SigApproxEntropy, ...
SigLyapExponent, ...
PeakFreq, ...
HighFreqPower, ...
EnvPower, ...
PeakSpecKurtosis, ...
'VariableNames', varnames);
endreset(ens)
% 加入特征名到集成数据元素中
ens.DataVariables = [ens.DataVariables; ...
"SigMean";"SigMedian";"SigRMS";"SigVar";"SigPeak";"SigPeak2Peak";"SigSkewness"; ...
"SigKurtosis";"SigCrestFactor";"SigMAD";"SigRangeCumSum";"SigCorrDimension";"SigApproxEntropy"; ...
"SigLyapExponent";"PeakFreq";"HighFreqPower";"EnvPower";"PeakSpecKurtosis"];
if runLocal
while hasdata(ens)
data = read(ens);
addData = analyzeData(data);
writeToLastMemberRead(ens,addData);
end
else
% 将集成数据分块进行并行运算
n = numpartitions(ens,gcp);
parfor ct = 1:n
subens = partition(ens,n,ct);
while hasdata(subens)
data = read(subens);
addData = analyzeData(data);
writeToLastMemberRead(subens,addData)
end
end
end第六步:故障分类特征选择
以上步骤计算得到的特征被用作构建分类器以分类不同故障工况。先配置集成对象以使其仅能读取提取得到的特征和故障标签
featureVariables = analyzeData('GetFeatureNames');
ens.DataVariables = [ens.DataVariables; featureVariables];
ens.SelectedVariables = [featureVariables; ens.ConditionVariables];
reset(ens)之后将集成数据对象存储中每个数据元素得到的特征集成为一个大的特征表
正在使用 Parallel Pool ‘local’ 计算 tall 表达式: - 第 1 次遍历(共 1 次): 用时 1 分钟 28 秒 计算已完成,用时 1 分钟 29 秒
对传感器漂移故障
用fscnca命令,将以上计算得到的所有特征作为预测变量,同时将传感器漂移故障标签做为响应(true或false响应)。fscnca命令返回每个特征的权值,权值大的特征代表预测标签时更重要。对传感器漂移故障来说,大权值指示着它们是有显著预测能力的特征,其他特征作用较小
idxResponse = strcmp(featureData.Properties.VariableNames,'SensorDrift');
idxLastFeature = find(idxResponse)-1; % 最后一个可作为潜在预测变量的特征索引
featureAnalysis = fscnca(featureData{:,1:idxLastFeature},featureData.SensorDrift);
featureAnalysis.FeatureWeightsidxSelectedFeature = featureAnalysis.FeatureWeights > 0.1;
classifySD = [featureData(:,idxSelectedFeature), featureData(:,idxResponse)]一组累计和范围值的柱状图可以说明为什么该特征是对传感器漂移故障识别有显著作用的
figure
histogram(classifySD.SigRangeCumSum(classifySD.SensorDrift),'BinWidth',5e3)
xlabel('Signal cumulative sum range')
ylabel('Count')
hold on
histogram(classifySD.SigRangeCumSum(~classifySD.SensorDrift),'BinWidth',5e3)
hold off
legend('Sensor drift fault','No sensor drift fault')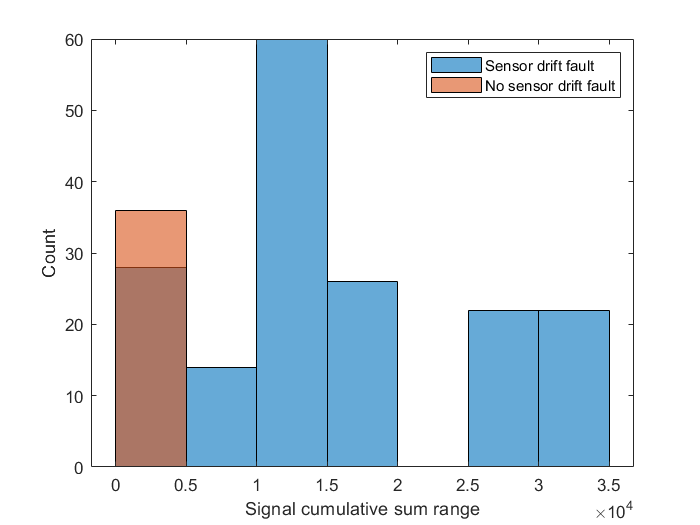
柱状图显示,信号累计和范围是一个对检测传感器漂移故障很好的特征,即使可能还需要另外的特征配合。因为当信号累计范围值小于0.5时,会有假阳现象出现
对轴磨损故障
同上过程,使用fscnca命令后得到三个对检测故障明显的故障,分别是信号李雅普诺夫指数、峰值频率和谱峭度中的峰值频率
idxResponse = strcmp(featureData.Properties.VariableNames,'ShaftWear');
featureAnalysis = fscnca(featureData{:,1:idxLastFeature},featureData.ShaftWear);
featureAnalysis.FeatureWeightsidxSelectedFeature = featureAnalysis.FeatureWeights > 0.1;
classifySW = [featureData(:,idxSelectedFeature), featureData(:,idxResponse)]信号李雅普诺夫分布柱状图显示了为什么单独使用这个特征不是好的预测变量
figure
histogram(classifySW.SigLyapExponent(classifySW.ShaftWear))
xlabel('Signal lyapunov exponent')
ylabel('Count')
hold on
histogram(classifySW.SigLyapExponent(~classifySW.ShaftWear))
hold off
legend('Shaft wear fault','No shaft wear fault')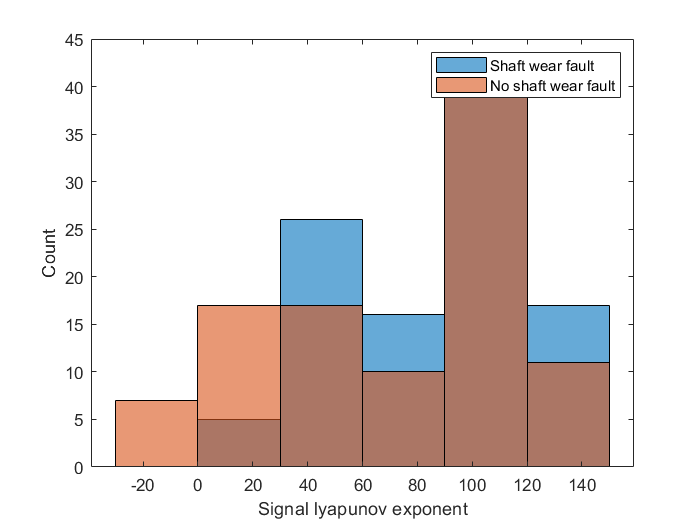
轴磨损故障特征选择说明了,对于这个故障类型的分类,选择多特征共同建模是有必要的。从上图中可以看出,即使是使用了最明显的特征作为预测变量,健康数据和故障数据的分布依然是很相似的,无法正确分类故障
对齿轮齿故障
fscnca命令显示,对于该故障同样有三个明显的特征可用,分别是信号累计和范围、信号李雅普诺夫指数和谱峭度中的峰值频率。选择这三个特征在分类齿轮齿故障时,表现不好,因此使用六个最重要的特征
idxResponse = strcmp(featureData.Properties.VariableNames,'ToothFault');
featureAnalysis = fscnca(featureData{:,1:idxLastFeature},featureData.ToothFault);
[~,idxSelectedFeature] = sort(featureAnalysis.FeatureWeights);
classifyTF = [featureData(:,idxSelectedFeature(end-5:end)), featureData(:,idxResponse)]figure
histogram(classifyTF.SigRangeCumSum(classifyTF.ToothFault))
xlabel('Signal cumulative sum range')
ylabel('Count')
hold on
histogram(classifyTF.SigRangeCumSum(~classifyTF.ToothFault))
hold off
legend('Gear tooth fault','No gear tooth fault')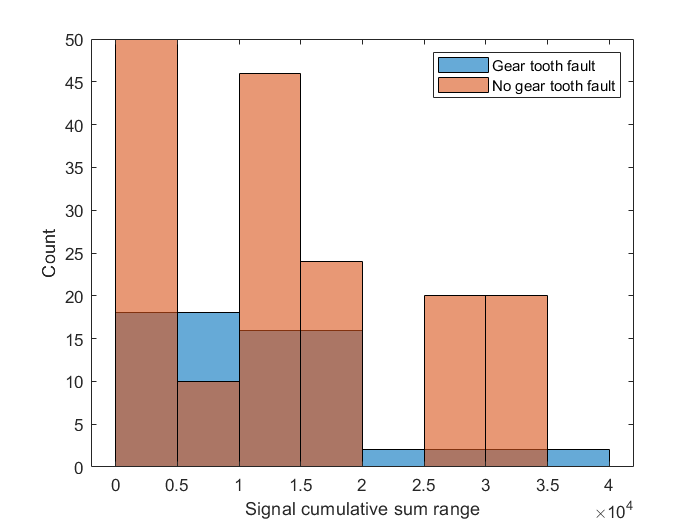
对上述结果,可以使用多项式核的支持向量机模型以分类齿轮齿故障。将特征表划分为训练、测试和验证数据集。用fitcsvm命令加以训练数据训练出一个支持向量分类器
rng('default') % 随机种子
cvp = cvpartition(size(classifyTF,1),'KFold',5); % 随机划分训练和验证数据
classifierTF = fitcsvm(...
classifyTF(cvp.training(1),1:end-1), ...
classifyTF(cvp.training(1),end), ...
'KernelFunction','polynomial', ...
'PolynomialOrder',2, ...
'KernelScale','auto', ...
'BoxConstraint',1, ...
'Standardize',true, ...
'ClassNames',[false; true]);用训练得到的模型使用predict方法对测试数据预测分类并使用混淆矩阵查看模型表现
% 将分类器应用于测试数据评估效果
actualValue = classifyTF{cvp.test(1),end};
predictedValue = predict(classifierTF, classifyTF(cvp.test(1),1:end-1));
% 画出混淆矩阵检验模型效果
confdata = confusionmat(actualValue,predictedValue);
h = heatmap(confdata, ...
'YLabel', 'Actual gear tooth fault', ...
'YDisplayLabels', {'False','True'}, ...
'XLabel', 'Predicted gear tooth fault', ...
'XDisplayLabels', {'False','True'}, ...
'ColorbarVisible','off'); 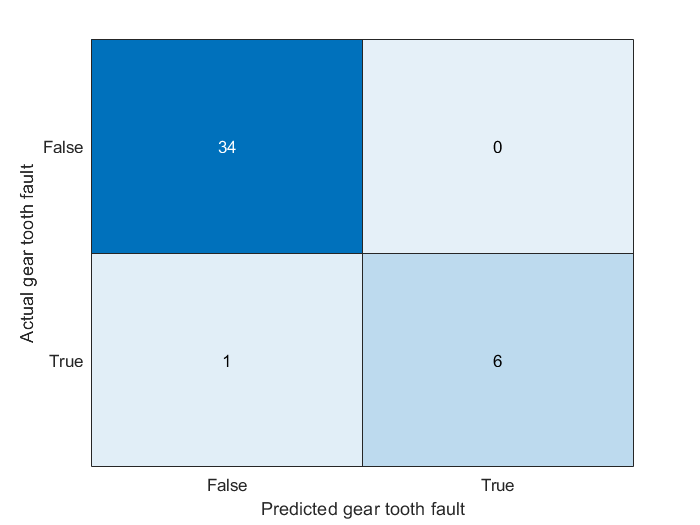
混淆矩阵可以看出,对无故障的数据都能正确识别出,但对于有齿轮齿故障数据,误将其中的一个样本划分成了无故障。这时,增加使用的特征数可以有效提升模型表现
第七步:总结
本案例展示了如何使用Simulink模拟故障数据,并使用集成对象清洗并提取数据特征,然后将被提取的特征用来建立分类器模型,以识别不同的故障类型
参考:https://ww2.mathworks.cn/help/predmaint/ug/Use-Simulink-to-Generate-Fault-Data.html