案例8：增广卡尔曼滤波方法用于故障检测

本案例了将介绍，如何使用增广卡尔曼滤波方法进行故障检测。本案例使用增广卡尔曼滤波方法应用于简单直流电机的摩擦力的在线估计。一旦估计出的摩擦力发生明显突变，将被视作故障。本案例使用系统识别工具箱中的函数，并不要求安装有预测性维护工具箱

第一步：电机建模

拥有转动惯量J，阻尼系数c的电机被扭矩u驱动。电机的角速度为ω，输出为角加速度ω̇。方程如下：
$$ \dot \omega = \frac{(u-c\omega)}J $$
为了利用增广卡尔曼滤波方法估计阻尼系数c，引入阻尼系数的辅助状态并将其导数设置为0 ，即ċ = 0
于是，模型状态量，x = [ω; c]，与测量量y = ω的关系方程如下： $$ \left[ \begin{matrix} \dot \omega \\ \dot c \end{matrix} \right]=\left[\begin{matrix} (u-c\omega)/J \\ 0 \end{matrix}\right] \\ y=\left[ \begin{matrix} \omega \\ (u-c\omega)/J \end{matrix} \right] $$


此时，时间连续的方程将使用近似估计的方法转化为离散方程，$\dot x=\frac{x_{n+1}-x_n}{T_s}$，其中Ts为离散采样周期。这样将被应用于pdmMotorModelStateFcn和pdmMotorModelMeasurementFcn函数中的离散模型方程如下：
$$ \left[\begin{matrix} \omega_{n+1} \\ c_{n+1} \end{matrix}\right] = \left[\begin{matrix} \omega_{n}+(u_n-c_n\omega_n)T_S/J \\ c_{n} \end{matrix}\right]\\ y_n=\left[\begin{matrix} \omega_n \\ (u_n-c_n\omega_n)/J \end{matrix}\right] $$
设定电机参数

设定初始状态

模型状态更新代码如下：

模型状态测量代码如下：

电机状态迁移时，历经状态（过程）噪声扰动q，同时还有测量噪声r，噪声部分可累加，方程更新如下：
$$ \left[\begin{matrix} \omega_{n+1}\\c_{n+1} \end{matrix} \right ]=\left[\begin{matrix} \omega_{n}+(u_n-c_n\omega_n)T_s/J\\c_{n} \end{matrix} \right ]+q\\ y_n=\left[\begin{matrix} \omega_{n}\\(u_{n}-c_n\omega_n)/J \end{matrix} \right ]+r $$
过程和测量噪声均值为0，即E[q] = E[r] = 0，同时协方差Q = E[qq′]，R = E[rr′]。摩擦力状态具有较高的噪声干扰水平。这也反映了这样一个事实，即我们希望摩擦力在电机运行时发生变化，并希望过滤方法能追踪这种状态。加速度和速度状态噪声水平较低，但速度和加速度的测量相对来说是有噪声干扰的

现在我们指定过程噪声的协方差

指定测量过程噪声的协方差

第二步：创建卡尔曼滤波

下面，创建增广卡尔曼滤波估计模型状态。我们尤其关注阻尼状态，因为该状态量的急剧变化指示着故障的发生

在Matlab中创建一个增广卡尔曼滤波extendedKalmanFilter对象，并且指定状态迁移和测量函数的雅各布矩阵

其中状态迁移和测量的雅各布函数如下：

增广卡尔曼滤波有事先定义的状态迁移和测量函数作为输入参数。初始状态值x0、初始状态协方差、测量和过程噪声协方差也都是增广卡尔曼滤波的输入。在本案例中，精确的雅各布函数能从状态迁移函数f和测量函数h中得到

第三步：模拟

为了模拟这一过程，创建一个循环，并在电机中引入故障（电机摩擦力的剧烈变化）。在循环中，使用增广卡尔曼滤波估计模型状态并特别追踪摩擦力的状态，以此检测摩擦力是否发生了显著变化

电机通过往复的脉冲串来进行加速和减速模拟，这种电机的操作模式类似于产线上的分拣机器人

模拟电机时，加入类似于构建增广卡尔曼滤波器时所使用的Q和R噪声协方差值的过程和测量噪声。对摩擦力，使用更小的摩擦力噪声值，因为摩擦力在非故障发生的情况下几乎恒定。仿真过程中人为地触发故障

使用状态更新方程模拟仿真模型，并将过程噪声添加到模型状态中。进入仿真10秒后，添加变化到电机摩擦力中。使用模型测量函数模拟电机传感器，并添加测量噪声到模型输出中

for ct = 1:numel(t)
   
   % 模型输出更新
   y = pdmMotorModelMeasurementFcn(x0,u(ct),J,Ts);
   y = y+Rv*randn(2,1);   % 添加测量噪声
   ySig(:,ct) = y;
   
   % 模型状态更新 
   xSigTrue(:,ct) = x0;
   x1 = pdmMotorModelStateFcn(x0,u(ct),J,Ts);
   % 引入摩擦力变化
   if t(ct) == 10
       x1(2) = 10;  % 阶跃变化
   end
   x1n = x1+Qv*randn(nx,1);  % 添加过程噪声
   x1n(2) = max(x1n(2),0.1); % 限定摩擦力的下界
   x0 = x1n; % 存储当前状态，为下一次迭代做准备
   
   % =================================================================
   % 以下部分将使用增广卡尔曼滤波进行状态估计
   % 要从电机的测量量中估计得到电机的状态量，使用增广卡尔曼滤波的predict和correct命令
   x_corr = correct(ekf,y,u(ct),J,Ts); % 基于当前测量值修正状态估计值
   xSigEst(:,ct) = x_corr;
   xstd(:,:,ct) = chol(ekf.StateCovariance);
   predict(ekf,u(ct),J,Ts);            % 给定当前状态和输入，预测下一状态量
   
   % =================================================================
   % 为检测摩擦力的变化，使用4s长度的滑动窗口计算摩擦力估计的均值和标准差。经过初始7秒时间后，锁定计算得到的均值和标准差。初始阶段计算得到的均值为无故障时的摩擦力均值。7秒后，如果估计得到的摩擦力大于无故障摩擦力均值超过3个标准差时，将被认定为摩擦力的显著变化。为减少噪声的影响和摩擦力估计的变化性，当和3σ边界对比时，使用摩擦力估计的均值
   if t(ct) < 7 
       % 计算摩擦力估计的均值和标准差
       idx = max(1,ct-400):max(1,ct-1); % Ts = 0.01 seconds
       fMean(ct) = mean( xSigEst(2, idx) );
       fSTD(ct)  = std( xSigEst(2, idx) );
   else
       % 存储计算得到的均值和标准差避免重复计算
       fMean(ct) = fMean(ct-1);
       fSTD(ct)  = fSTD(ct-1);
       % 使用期望的摩擦力均值和标准差检测摩擦力变化
       estFriction = mean(xSigEst(2,max(1,ct-10):ct));
       fChanged(ct) = (estFriction > fMean(ct)+3*fSTD(ct)) || (estFriction < fMean(ct)-3*fSTD(ct));
   end
   if fChanged(ct) && ~fChanged(ct-1) 
       % 检测摩擦力变化信号的上升沿 |fChanged|.
       fprintf('Significant friction change at %f\n',t(ct));
   end
   % =================================================================
   % 使用估计得到的状态计算输出估计。计算测量和估计输出的误差，并计算误差的统计信息。误差的统计信息可以被用来检测摩擦力变化。稍后将详细讨论
   ySigEst(:,ct) = pdmMotorModelMeasurementFcn(x_corr,u(ct),J,Ts);   
   idx = max(1,ct-400):ct;
   fKur(:,ct) = [...
       kurtosis(ySigEst(1,idx)-ySig(1,idx)); ...
       kurtosis(ySigEst(2,idx)-ySig(2,idx))];
end

第四步：增广卡尔曼滤波方法表现

可以看出，摩擦力变化发生在10.45秒时。接下来，我们将描述该故障检测规则如何产生。首先检验仿真结果和过滤器表现

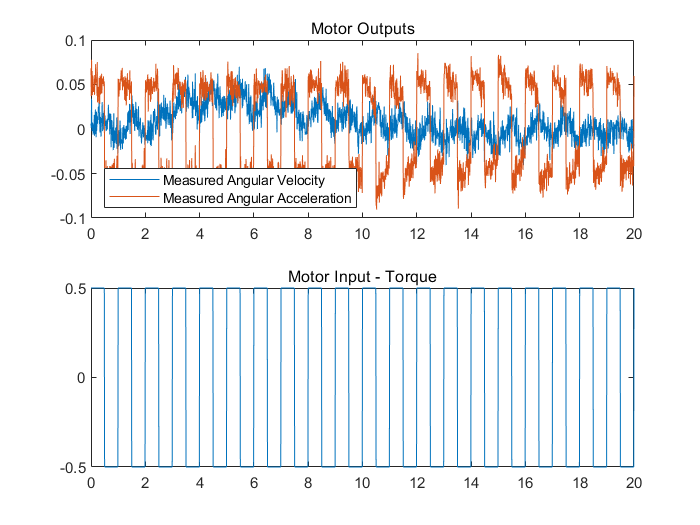
模型输入输出显示，很难直接从测量信号中检测到摩擦力的变化。增广卡尔曼滤波方法是我们能估计到系统状态，尤其是摩擦力的状态

下面我们可以比较真实模型状态和估计得到的状态。估计得到的状态展示时，加上了3σ置信区间

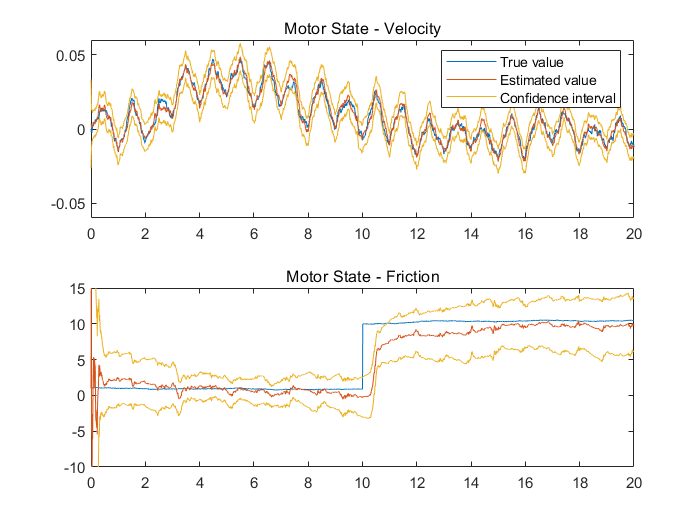
可以看出，滤波器估计追踪着真实值，同时保有有界的置信区间。对估计误差的检验将为我们提供更多反映滤波器表现的内容

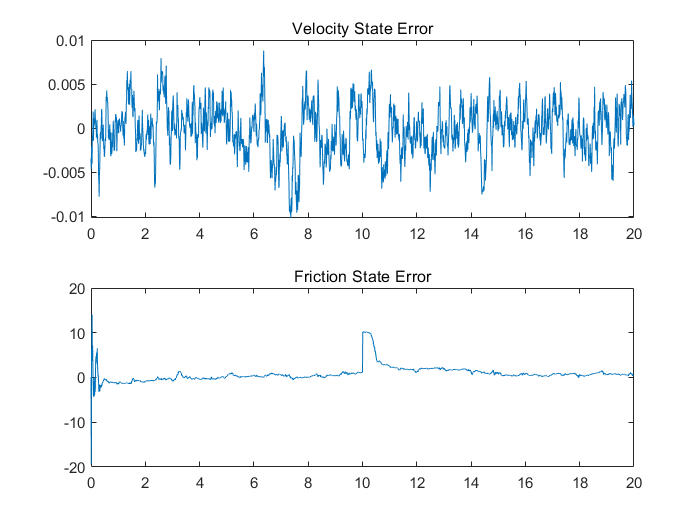
误差曲线表明，滤波器能适应10秒时的摩擦力变化，随后能将估计误差降低到0。然而误差曲线却不能用来做故障检测，因为它们的绘制依赖于真是状态值

比较测量状态值和加速度、速度的估计状态值，可以建立故障检测机制

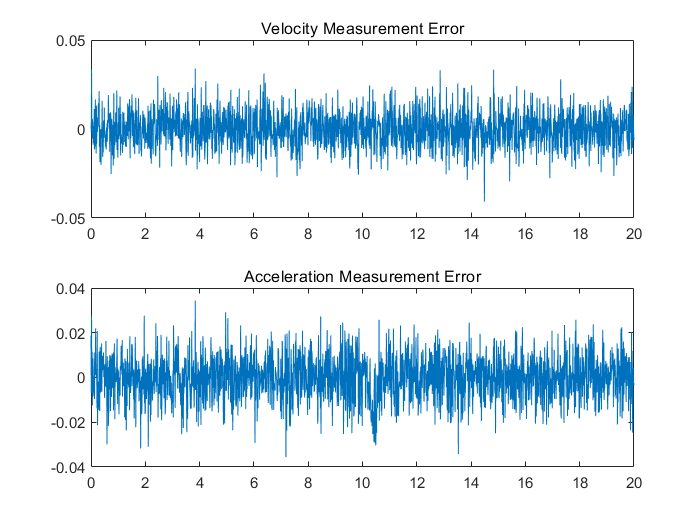
在10秒引入故障时，加速度误差曲线表现出微小的误差均值变化。可以看看该误差项的统计信息，判断通过它是否能够检测出故障。加速度和速度误差通常属于正太分布（噪声模型都服从高斯模型）。因此，当误差分布因为摩擦力的变化并导致误差分布发生变化时，误差分布可能会从对称变化为非对称时，这时加速度误差的峰度也许可以帮助识别故障

忽略前4秒，因此时估计器还在收敛过程中，且数据正在逐步收集，此时误差的峰度在3的附近微小变动，这正对应着标准高斯分布的峰度值（3σ）。这样的话，误差的统计信息在此案例中便不能用于自动化故障检测。在此应用中，使用误差的峰度也是很难的，因为过滤器是逐步适应的，并且不断地将误差降为0，只有在给出短时间窗口时，其误差分布才不同于0

于是在本应用例子中，使用摩擦力的估计值地变化便能最好地自动化检测电机故障。使用已知无故障数据得到的摩擦力的估计值（均值和标准差）可以构建摩擦力的预期边界（3σ边界），这使得当边界条件被打破时，故障检测变得简单。以下绘图突出了这一故障检测方法

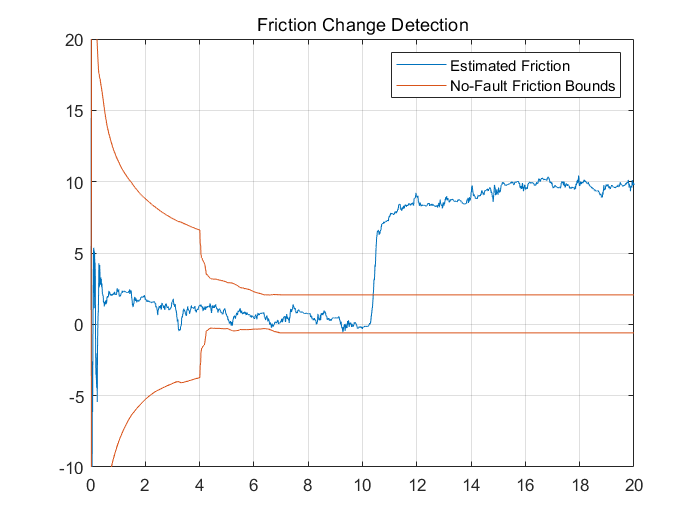
第五步：总结

本例展示了如何使用增广卡尔曼滤波器估计简单直流电机的摩擦力，并将该摩擦力用于故障检测

参考：https://ww2.mathworks.cn/help/predmaint/ug/Fault-Detection-Using-an-Extended-Kalman-Filter.html