案例3：使用稳态实验进行离心泵故障诊断

该案例展示了如何使用基于模型的方法进行不同类型故障的监测和诊断，该案例遵循Rolf Isermann在故障诊断应用程序一书中给出的离心泵分析

第一步：离心泵相关先验知识介绍

离心泵用途：离心泵通过将来自电机或内燃机产生的旋转动能转化为流体的流体动能来达到输送液体的目的，液体进入泵叶轮后被叶轮加速，并呈放射状向外流入扩散器

离心泵常见故障：

  • 气穴现象：流体内部形成的气泡破裂时可能会导致叶轮损伤
  • 液体中溶解有气体：压降导致的气体溶解于液体中
  • 空转：无液体进入导致缺乏冷却或轴承过温
  • 物理侵蚀：硬颗粒或气穴导致的泵体损伤
  • 化学腐蚀：腐蚀性液体导致的损伤
  • 轴承磨损：通过金属磨损、金属疲劳、点蚀导致的机械损伤
  • 减压孔堵塞：导致过载或破坏轴向轴承
  • 滑动环密封堵塞：导致更强的摩擦和更低的工作效率
  • 密封破损的增加：导致效率损失
  • 沉积：有机物沉淀或其他化学反应生成物沉淀
  • 震荡：转子损坏或沉积导致的转子不平衡，会造成轴承损伤

典型可用的传感器：

  • 入口和出口的压强差Δp

  • 转速ω
  • 电机或发动机转矩Mmot和泵转矩Mp
  • 泵出口的液体流出率Q
  • 驱动电机电流、电压、温度

  • 液体温度、沉积物

第二步：泵和管路系统的数学模型

由欧拉涡轮方程得到如下压差Δp，转速ω，液体流出率Q的关系：
Hth?=?h1ω2???h2ωQ
其中$H_{th}=\frac{\Delta p}{\rho g}$表示理论扬程（理想状态下无损失），单位为米。h1和h2是比例常数。考虑摩擦损失和冲击损失时，实际扬程为：
H?=?hnnω2???hnvωQ???hvvQ2
此处，hnn，hnv，hvv是被看作是模型参数的比例常数。对应的泵扭矩为：
$$ M_p=\rho g(h_{nn}\omega Q-h_{nv}Q^2-h_{vv}\frac{Q^3}{\omega}) $$
当电机和泵机械部分施加的扭矩使转速提升时，满足以下关系：
$$ J_p\frac{d\omega (t)}{dt}=M_{mot}(t)-M_p(t)-M_f(t) $$

此处，JP为电机和泵的惯量比，Mf由库仑摩擦力矩Mf0和粘性摩擦力矩Mf1ω(t)组成：
Mf(t)?=?Mf0sign(ω(t))?+?Mf1ω(t)
同时，泵被连接到管道系统中，并将液体从较低的储罐传输到较高的储罐。力矩平衡方程如下：
$$ H(t)=a_F\frac{dQ(t)}{dt}+h_{rr}Q^2(t)+H_{static} $$
此处，hrr为管道系统的阻力系数，$a_F=\frac{l}{gA}$，l表示管道长度，A表示管道横截面积，Hstatic表示泵上的储存高度。模型参数hnn、hnv、hvv要么从物理学知识方面得到，要么通过将测量到的传感器信号放入模型的输入/输出中进行拟合估计得到。所使用的模型可能取决于泵运行时的操作工况，例如当泵总是以恒定角速度运行时，则可能不需要使用泵-管道系统的完整非线性模型

第三步：相关故障检测技术

故障检测可通过比较从测量数据中提取的特定特征值和正常运行时得到的阈值的差实现。此时，不同故障的可检测性、可分离性取决于实验的性质和测量的可用性。比如，带压力监测的恒速分析只能检测引发较大压力变化的故障，然而它并不能有效评估故障发生原因。这时，通过测量压差、电机转矩和液体流出率可以检测和分离许多故障源，如气穴、空转、大的沉积、电机故障等

基于模型的方法使用以下技术：

  1. 参数估计：使用来自健康状态（标称）的测量数据建模，估计出模型参数并对其不确定性进行量化。然后，测试系统测得数据被重新估计得到参数值，该参数值被用来和标称值（标称状态得到的模型参数估计）对比诊断故障。该技术便是本案例讨论的话题
  2. 残差生成：先对健康状态数据建模得到模型，然后通过模型在测试系统上的输出和测试系统测得的实际观测量做残差计算得到残差信号，之后分析残差信号的峰值、方差及其他特性来检测故障。可以设计不同的残差用来区分不同故障源导致的故障。该技术在案例4中讨论

第四步：恒速实验——通过参数估计进行故障分析

一种对泵进行校准和监测的常见方法是使泵以恒定的角速度运行，并记录泵的静压头和液体流出率。通过改变管道系统阀门位置，液体流出体积可以被调节。流量的增加会造成泵扬程的减少，该泵测量得到的扬程特性可以被用来和供应商提供的数据值对比，其中产生的任意差值都可能指示着潜在的故障。通过Simulink中管道-泵系统的模拟，可以获得输出水头和液体流出率的测量值

当标称转速为2900 RPM时，理想状态下供应商提供的健康水泵的泵扬程特性如下所示：

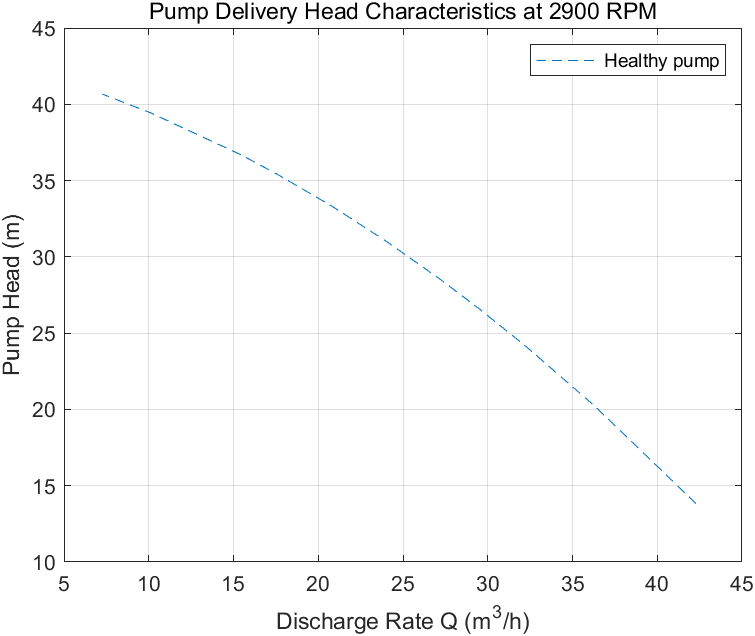
能导致泵特性明显改变的故障如下：

  1. 间隙处的磨损
  2. 叶轮出口的磨损
  3. 叶轮出口的沉积物

分析故障水泵时，受不同故障程度影响水泵的转速、转矩、液体流出率等测量数据被记录。例如当故障源发生在间隙垫圈时，测量得到的泵扬程特性在特性曲线上表现为明显的移位，如下：

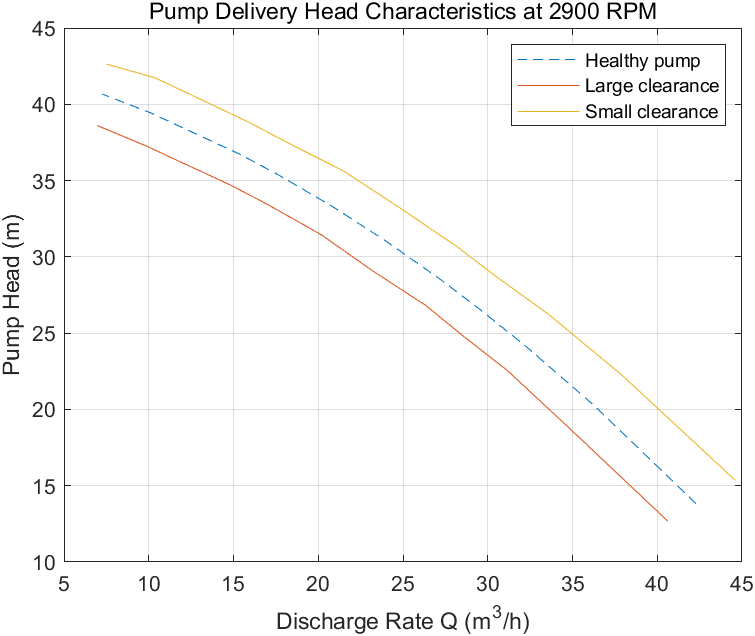
类似的变化也可以从转矩-流量特性和其他故障类型中看到

对于自动化故障诊断，需要将观察得到的变化转化为定量信息。其中一种可行的方案是将参数化曲线于上图所示的扬程-水流特性曲线中拟合。利用泵-管道动力学控制方程，并利用简化的扭矩关系，得到以下方程：
$$ H\approx h_{nn}\omega^2-h_{nv}\omega Q-h_{vv}Q^2 \\ M_p\approx k_0\omega Q-k_1Q^2+k_2\omega^2 $$
其中，hnn，hnv，hvv，k0，k1，k2 e">Q，H和MP的值，这些参数可以用线性最小二乘估计得到。此时，这些参数便是用来开发故障检测和诊断算法的特征

第五步：初步分析——比较参数值

计算并画出上图3条曲线对应的参数估计值，Q，H和MP使用测量值，ω?=?2900RPM作为标称泵转速

得到结果如下：

其中linearFit为定义的外部函数，如下：

k0，k1，k2的估计值展示如下：

由结果分析出以下三点：

  • 随着间隙距较大时，hnn和k0取值减小，但对于小间隙的情况又大于标称值
  • hvv和k2的值对于大间隙变大，对于小间隙变小
  • hnv和k1对于间隙距的依赖关系不明

第六步：考虑不确定性分析

初步分析的结果展示了模型参数如何随故障情况的变化而变化。然而，即使对于健康水泵，测量导致的噪点，流体污染，粘度变化以及电机运行时的滑转扭矩特性等因素都会对测量数据造成偏差。这些测量时的变数都给参数估计带来了不确定型

现采集五组来自健康无故障运行在2900 RPM转速下同时调节节流阀处于10个不同位置的水泵数据，如下：

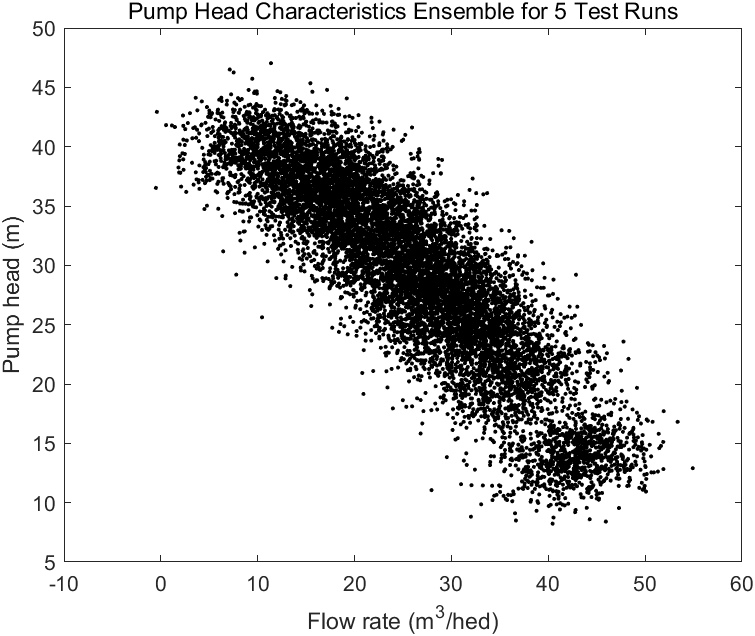
图像显示即使对于运行于实际工况中的健康水泵，特性曲线也会有较大偏差，这种偏差应该在诊断模型建模时被考虑到。下一节将讨论这种情况下的故障诊断和带噪点数据分离的技术

第七步：异常检测

在大多数情形下，往往只能获得健康水泵数据。在这种情况下，可以使用可用测量数据来创建健康状态的统计描述，如使用参数向量的均值和协方差等。之后将测试水泵的测量数据和得到的标称统计结果进行对比，依次确定测试水泵是否健康。通常，故障水泵测试数据得到的特征值会被检测为异常值

以下代码用来估计泵扬程和扭矩参数值的均值和协方差

之后便可可视化估计得到的模型参数值，因测量得到数据的不确定性，此处加上一个置信度为74%的置信区间，相对应着两个标准差（$\sqrt{chi2inv(0.74,3)}\approx2$，3表示自由度，此过程为卡方分布中的已知置信度和自由度求范围的问题）

绘图前，先定义一个画三维平面的函数如下：

之后画出hnn，hnv，hvv三个模型参数构成的椭圆平面

以及k0，k1，k2三个模型参数构成的椭圆平面

得到图像如下：

这两个椭圆面基本框定了hnn，hnv，hvv，k0，k1，k2六个模型参数值在74%置信区间时的正常值范围

对之后测量得到的水泵数据，可通过同样的处理把散点绘制到图像中，如下加载测试数据后的情况：

测试数据中包含了一组10条时序测量数据，表征了水泵阀门处于10个不同位置时的水泵转速、扭矩、扬程和流出率数据。所有测试数据对应的水泵都有不同程度的间隙缝问题

现查看其中一条数据的前5个时间点如下：

对测试数据，同样画出他们估计得到的模型参数值相对于正常值范围的图像如下：

从图上可以看出，哪些位于椭圆外部的绿色点可以看作异常点，椭圆内的点可能来自健康水泵或者逃过了针对该故障模式检测的异常水泵（即该方法不适用于其他泵异常情况）。同时可以看出，有些在泵扬程模型参数图中的异常点在泵扭矩模型参数图中不一定会被认定为异常点，这可能是因为左图和右图能检测到的故障源不同，或者压力和扭矩的测量存在潜在的可靠性问题

第八步：使用置信区域定量化异常检测

至此仍然存在一个问题，故障程度的评估，可简单理解为第七步中的点距离椭圆面的距离该如何量化描述。此时马氏距离mahal可以被用来描述测试样本距离正常样本的偏离程度，如下：

当使用74%作为可接受的健康数据参数偏差时，任意在ParDist1中大于22?=?4的值都将被视为异常值（因为通过函数mahal计算得到的是马氏距离的平方，而2表示卡方分布中，74%置信区间位置相对均值的偏离值，即马氏距离平方为22?=?4），即指示着泵故障

下面将这些距离值加入到上述的绘图中，异常值将被标注为红线，在此之前再次引入一个外部函数helperAddDistanceLines用来给点到椭圆的距离度量加上实线表示

对泵扬程数据，结果如下：

对泵扭矩数据，结果如下：

将结果绘制到椭圆面图像中：

这样，不仅能识别水泵是否有故障，同时还能量化故障的严重程度

第九步：使用一类支持向量机（one-class SVM）算法定量化异常检测

另一种有效的方式便是使用健康水泵得到的模型参数估计值建立一类支持向量机（one-class SVM）分类算法模型，该算法一般用做异常点检测，训练数据都属于一类，即健康数据。如前面得出的结论所述，hnn，hvv在指示潜在故障方面更明显，因此使用这两个变量作为分类算法的输入

模型拟合完成后，通过以下代码可视化模型边界及各个测试点相对模型的位置

绘图函数helperPlotSVM如下：

针对泵扬程模型参数的可视化结果如下：

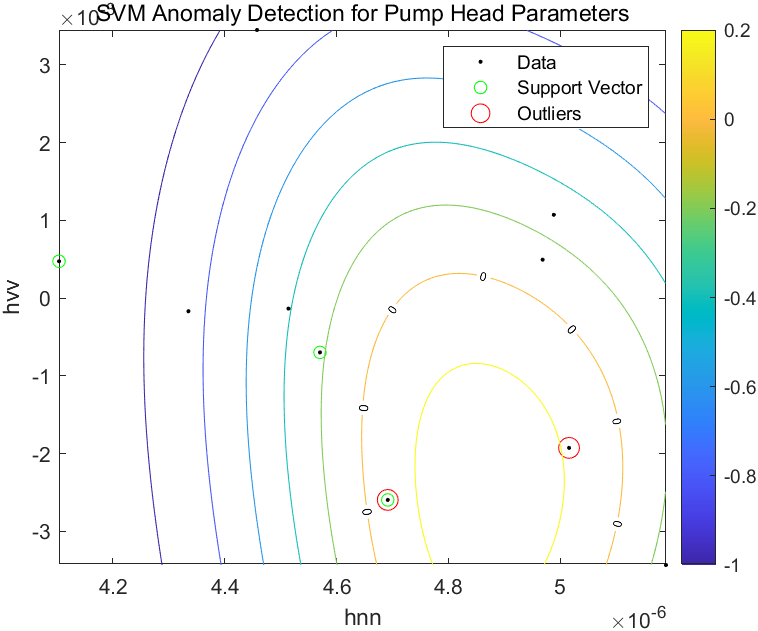
针对泵扭矩模型参数的可视化结果如下：

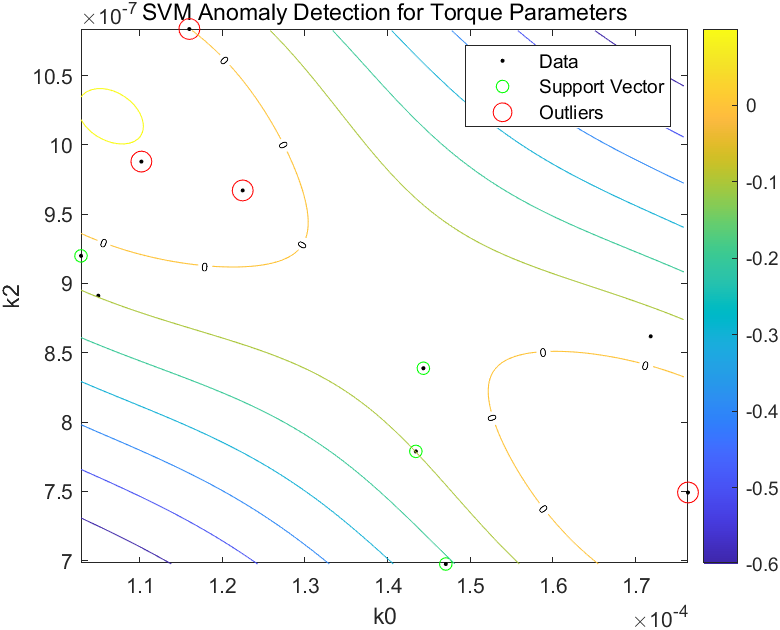
两图中，等高线0以内的数据点都被认定为异常点

第十步：以稳态参数为特征进行故障分离

假如测试故障水泵的故障类型可知时，可以开发出不但能检测到故障而且能识别故障类型的算法

使用似然比检验区分间隙距故障

首先，可将间隙距的变化划分为两大类，变大和变小（泵扬程特性曲线中的红线和黄线）。之后加载测试水泵数据，这些水泵的间隙距事先都已知晓（变大或变小）。最后便可以依此建立一个三大类的分类模型，这三类分别是：

  • 正常间距（健康水泵）
  • 大间距
  • 小间距

代码如下：

该集成数据包含了50个水泵数据（50次独立实验），之后像之前一样使用线性稳态模型拟合并得到针对泵扬程和扭矩数据的模型参数估计值

之后使用柱形图函数helperPlotHistogram可视化得到的模型参数估计值的分布图

function helperPlotHistogram(Theta1, Theta2, Theta3, names)
%helperPlotHistogram Plot histograms of pump parameters.
%
% This function is only in support of
% CentrifugalPumpFaultDiagnosisUsingSteadyStateExperimentsExample. It may
% change in a future release.

% Copyright 2017 The MathWorks, Inc.
f = figure;
subplot(311)
localAdjustMarkers(histfit(Theta1(:,1)));
hold on
localAdjustMarkers(histfit(Theta2(:,1)))
localAdjustMarkers(histfit(Theta3(:,1)))
ylabel(names{1})
if strcmp(names{1},'hnn')
   title('Fault Mode Histograms: Head Parameters')
else
   title('Fault Mode Histograms: Torque Parameters')
end
L = findall(gca,'Type','line','Tag','PDF');
uistack(L,'top');

subplot(312)
hg = histfit(Theta1(:,2));
hasbehavior(hg(2),'legend',false)
localAdjustMarkers(hg)
hold on
hg = histfit(Theta2(:,2));
hasbehavior(hg(2),'legend',false)
localAdjustMarkers(hg)
hg = histfit(Theta3(:,2));
hasbehavior(hg(2),'legend',false);
localAdjustMarkers(hg)
ylabel(names{2})
legend('Healthy','Large', 'Small')
L = findall(gca,'Type','line','Tag','PDF');
uistack(L,'top');

subplot(313)
localAdjustMarkers(histfit(Theta1(:,3)))
hold on
localAdjustMarkers(histfit(Theta2(:,3)))
localAdjustMarkers(histfit(Theta3(:,3)))
ylabel(names{3})
L = findall(gca,'Type','line','Tag','PDF');
uistack(L,'top');

f.Position(4) = f.Position(4)*1.8571;
centerfig(f)

%--------------------------------------------------------------------------
function localAdjustMarkers(hh)
% 配置概率密度函数曲线标记以提升可读性

Col = hh(1).FaceColor;
hh(2).Color = Col*0.7;
hh(1).FaceColor = min(Col*1.2,[1 1 1]);
hh(1).EdgeColor = Col*0.9;
hh(1).FaceAlpha = 0.5;
hh(2).Tag = 'PDF';

泵扬程模型参数分布图：

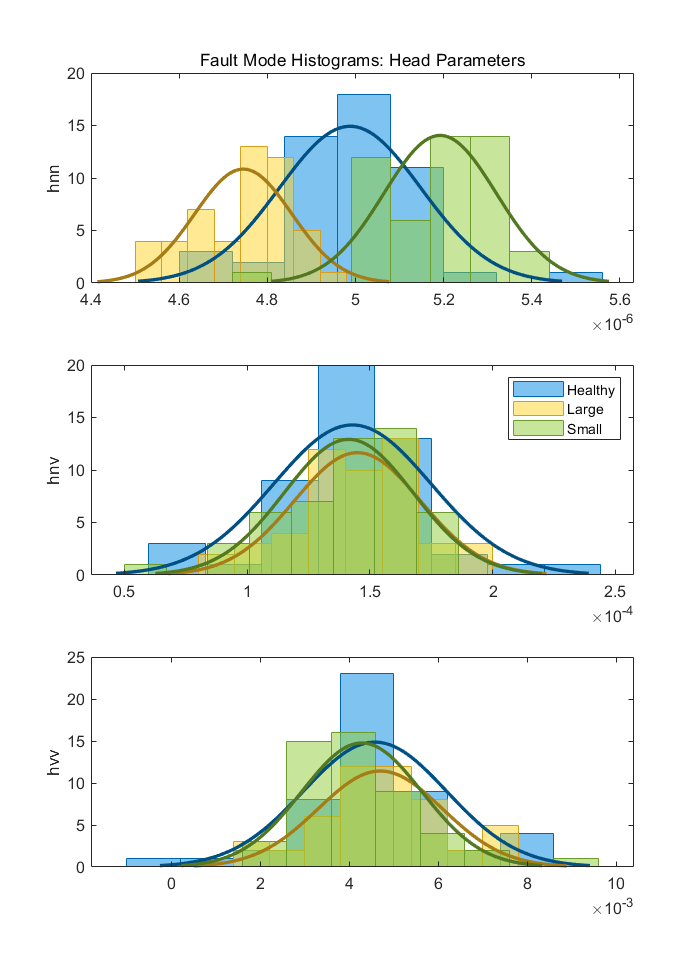
图上结果显示，参数hnn具有比较好的故障模式分离能力，参数hnv和hvv的概率密度函数在三种模式下具有较大的重叠部分，不太合适用来分离这三种故障模式

泵扭矩模型参数分布图：

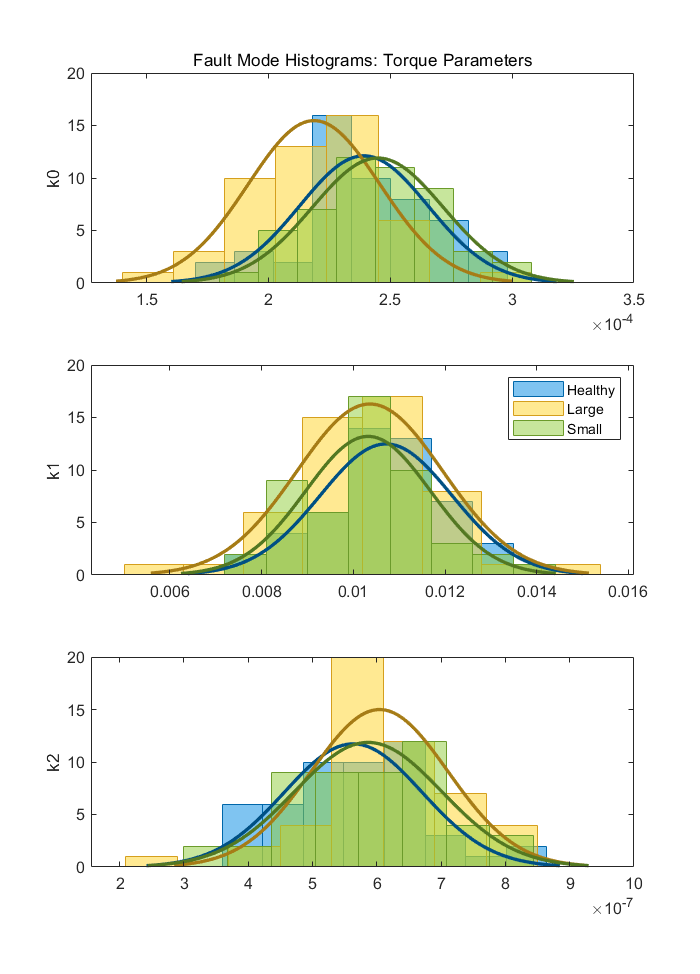
从上图可以看出，对于泵扭矩模型估计参数分布来说，k0，k1，k2三个参数都不太能很好地区分三种故障模式。好在均值和方差方面的一些变化依然可以很好地被三类分类器使用。假如概率密度函数在均值和方差的分离方面表现出了比较好的能力，便可以设计一个似然比检验评估测试数据更可能属于哪一类

首先设定三个假说：

  • H0：泵扬程模型参数属于正常水泵
  • H1：泵扬程模型参数属于大间隙水泵
  • H2：泵扬程模型参数属于小间隙水泵

之后测试数据得到的模型参数，该数据的类被分配给三个函数中概率密度函数值最大的那一类，例如假设H0成立即参数的类为正常水泵，则p(H0)?>?p(H1)。之后得到的结果按照真实值和预测值画出混淆矩阵如下（最大似然检验函数定义为pumpModeLikelihoodTest）：

function pumpModeLikelihoodTest(HealthyTheta, LargeTheta, SmallTheta)
%pumpModeLikelihoodTest Generate predictions based on PDF values and plot confusion matrix.
%mvnpdf函数用来计算概率密度函数值

m1 = mean(HealthyTheta);
c1 = cov(HealthyTheta);
m2 = mean(LargeTheta);
c2 = cov(LargeTheta);
m3 = mean(SmallTheta);
c3 = cov(SmallTheta);

N = size(HealthyTheta,1);

% True classes
% 1: Healthy: group label is 1.
X1t = ones(N,1);
% 2: Large gap: group label is 2.
X2t = 2*ones(N,1);
% 3: Small gap: group label is 3.
X3t = 3*ones(N,1);

% Compute predicted classes as those for which the joint PDF has the maximum value.
X1 = zeros(N,3); 
X2 = zeros(N,3); 
X3 = zeros(N,3); 
for ct = 1:N
   % Membership probability density for healthy parameter sample
   HealthySample  = HealthyTheta(ct,:);
   x1 = mvnpdf(HealthySample, m1, c1);
   x2 = mvnpdf(HealthySample, m2, c2);
   x3 = mvnpdf(HealthySample, m3, c3);
   X1(ct,:) = [x1 x2 x3];
   
   % Membership probability density for large gap pump parameter
   LargeSample  = LargeTheta(ct,:);
   x1 = mvnpdf(LargeSample, m1, c1);
   x2 = mvnpdf(LargeSample, m2, c2);
   x3 = mvnpdf(LargeSample, m3, c3);
   X2(ct,:) = [x1 x2 x3];
   
   % Membership probability density for small gap pump parameter
   SmallSample  = SmallTheta(ct,:);
   x1 = mvnpdf(SmallSample, m1, c1);  
   x2 = mvnpdf(SmallSample, m2, c2);
   x3 = mvnpdf(SmallSample, m3, c3);
   X3(ct,:) = [x1 x2 x3];
end

[~,PredictedGroup] = max([X1;X2;X3],[],2);
TrueGroup = [X1t; X2t; X3t];
C = confusionmat(TrueGroup,PredictedGroup);
heatmap(C, ...
    'YLabel', 'Actual condition', ...
    'YDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ...
    'XLabel', 'Predicted condition', ...
    'XDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ...
    'ColorbarVisible','off');
end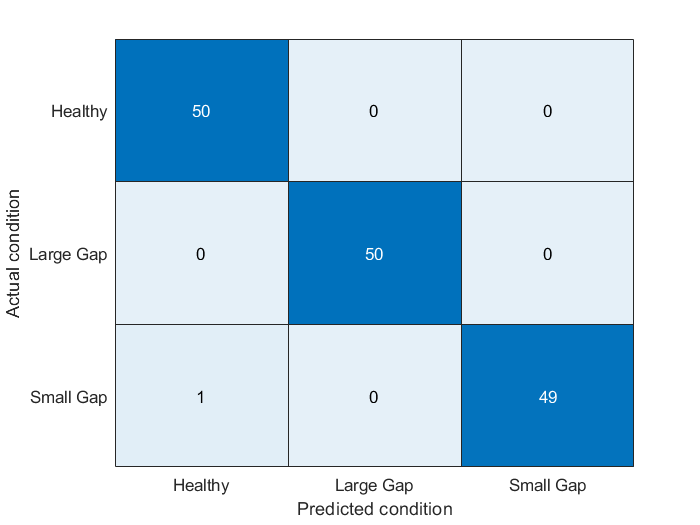

混淆矩阵显示，各种故障模式被很好的分离，这一点从hnn的分布图象中也能看出

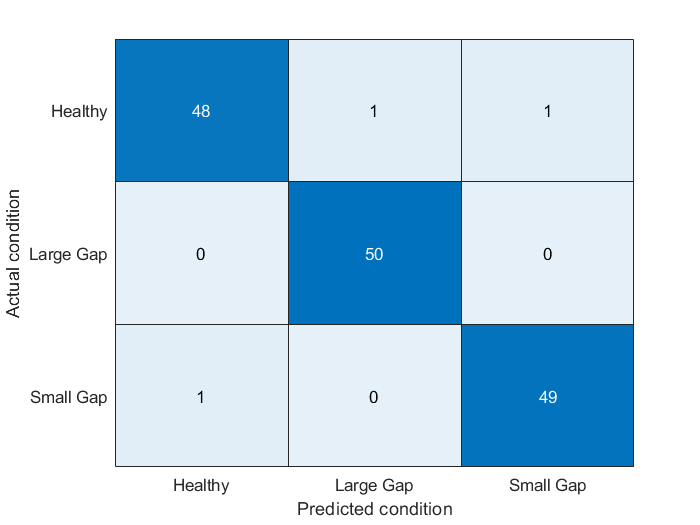
相比泵扬程的结果，泵扭矩的结果稍稍差一点，但依然有比较高的97%分类正确率，即使从参数分布的图像看来，三种模式具有很多的重合部分。这是因为概率密度函数值的计算不仅被均值影响也会被方差影响（意思是虽然从均值是看三者比较接近，但结合方差信息后便能比较好的区分）

使用Bagging树模型做故障模式多分类

当需要将故障从一堆故障模式中确定出来时，本方法更合适。考虑以下模式：

  1. 健康
  2. 间隙距磨损
  3. 叶轮出口小量沉积
  4. 叶轮进口沉积
  5. 叶轮出口物理磨损
  6. 叶片折断
  7. 气穴

此时，分类问题变的困难，因为可用的参数尚且只有3种，而操作模式有7种。

这时，就可以使用Bagging树分类模型（基于决策树的集成算法，随机森林便是Baggin树模型的进阶版本）加以区分。输入为来自以上7种情况下，50条带标记的数据。先对每条数据估计得到参数，然后使用来自每种模式的参数估计子集来训练分类器，代码如下：

load MultipleFaultsData
% 计算泵扬程参数
HealthyTheta = linearFit(1, HealthyEnsemble);
Fault1Theta  = linearFit(1, Fault1Ensemble);
Fault2Theta  = linearFit(1, Fault2Ensemble);
Fault3Theta  = linearFit(1, Fault3Ensemble);
Fault4Theta  = linearFit(1, Fault4Ensemble);
Fault5Theta  = linearFit(1, Fault5Ensemble);
Fault6Theta  = linearFit(1, Fault6Ensemble);

% 对每种操作工况打上对应的标签
Label = {'Healthy','ClearanceGapWear','ImpellerOutletDeposit',...
    'ImpellerInletDeposit','AbrasiveWear','BrokenBlade','Cavitation'};
VarNames = {'hnn','hnv','hvv','Condition'};
% 将参数和对应的标签集成为table型数据
N = 50; 
T0 = [array2table(HealthyTheta),repmat(Label(1),[N,1])];
T0.Properties.VariableNames = VarNames;
T1 = [array2table(Fault1Theta), repmat(Label(2),[N,1])];
T1.Properties.VariableNames = VarNames;
T2 = [array2table(Fault2Theta), repmat(Label(3),[N,1])];
T2.Properties.VariableNames = VarNames;
T3 = [array2table(Fault3Theta), repmat(Label(4),[N,1])];
T3.Properties.VariableNames = VarNames;
T4 = [array2table(Fault4Theta), repmat(Label(5),[N,1])];
T4.Properties.VariableNames = VarNames;
T5 = [array2table(Fault5Theta), repmat(Label(6),[N,1])];
T5.Properties.VariableNames = VarNames;
T6 = [array2table(Fault6Theta), repmat(Label(7),[N,1])];
T6.Properties.VariableNames = VarNames;

% 堆叠所有数据
% 从50条种选出30条建模
TrainingData = [T0(1:30,:);T1(1:30,:);T2(1:30,:);T3(1:30,:);T4(1:30,:);T5(1:30,:);T6(1:30,:)];

% 使用模型参数建立拥有20棵子决策树的集成模型
rng(3) % 为了可再现设置的随机种子
Mdl = TreeBagger(20, TrainingData, 'Condition',...
   'OOBPrediction','on',...
   'OOBPredictorImportance','on')

得到如下模型：

装袋决策树模型的表现可以通过研究袋外观测的误分类率和树棵数的函数关系来体现，如下：

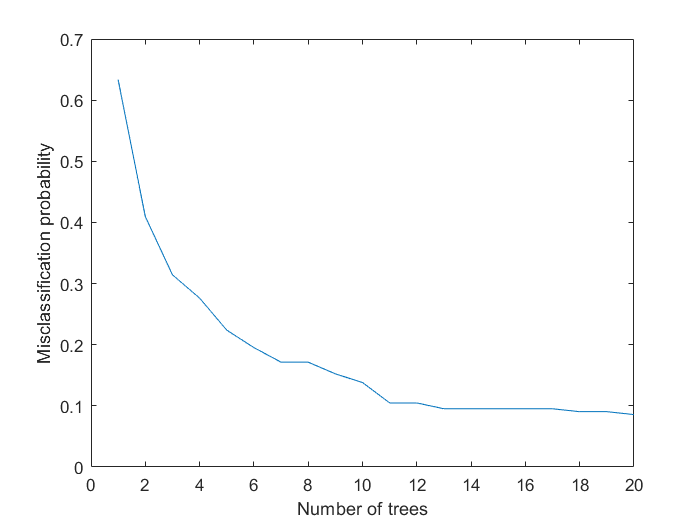
最后，使用未知的测试数据检验模型表现

第十一步：总结

好的故障诊断策略能很好的减少宕机时间和部件更换成本，这依赖于丰富的对系统认知的专家知识，它可以结合测量得到的传感器数据来检测和分离不同的故障

在本案例中，基于对水泵运行的动力学模型的了解以及参数估计方法得到了模型对应的参数估计值，之后使用这些值作为训练数据训练开发新的故障诊断算法，如异常检测算法，似然比检测，多分类器等

为了更好地将这些知识应用于其他方面，现总结整个案例过程如下：

  1. 将水泵运行至标称转速2900 RPM，调节节流阀值不同位置，记下对应的液体流出率、泵转速、压差和扭矩
  2. 估计泵扬程和泵扭矩对应方程中的参数
  3. 假如不确定性水平（或称噪音水平）较低，并且参数估计值可靠，便可以直接用该值对比得到的标称值，两者之间的差代表了故障性质
  4. 对一般有噪声的情况下，首先用异常检测方法判断是否真的有故障存在于系统中。这一步可以通过对比得到的参数估计值和它们在泵健康情况下得到的历史均值和协方差判断
  5. 如果有故障，使用故障分类方法（如似然比检验或多分类模型）分离可能的故障源。分类方法的选择可取决于传感器数据的可用性、可靠性、故障严重性、基于故障模式的历史信息（比如有对应标签的数据）可用性

参考：https://ww2.mathworks.cn/help/predmaint/ug/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments.html