案例4:使用残差分析进行离心泵故障诊断
本案例延续了案例3中基于稳态实验的故障诊断方法的情况,所不同的是本案例中的水泵运行于各种不同工况中,即转速不再限于2900 RPM
第一步:多速泵系统建模——基于残差分析的诊断
当水泵运行于转速变化快且变化范围大时,稳态泵扬程和扭矩方程不再能得到精确结果。此时,摩擦和其他损失的影响变得更加明显,而模型参数又依赖水泵转速。可行的方案便是建立一个黑盒模型,模型参数不必具有物理意义。该模型作为水泵已知行为的模拟器,模型的输出为从对应的测量信号中提取得到的残差。残差的特性,如均值、方差和功率被用来区分正常和故障操作工况
由如下系统简图可知,使用静态泵扬程方程,动态泵-管道系统方程,可以计算出图中标红的4种残差

系统图中四个灰色模型的表示如下:
- 静态泵模型:Δp̂(t) = θ1ω2(t) + θ2ω(t)
- 动态管道模型:$\hat Q(t)=\theta_3+\theta_4\sqrt{\Delta p(t)}+\theta_5\hat Q(t-1)$
- 动态泵-管道模型:$\hat{\hat Q}(t)=\theta_3+\theta_4\sqrt{\Delta\hat p(t)}+\theta_5\hat{\hat Q}(t-1)$
- 动态逆泵模型:M̂motor(t) = θ6 + θ7ω(t) + θ8ω(t − 1) + θ9ω2(t) + θ10M̂motor(t − 1)
模型参数θ1, ..., θ10与水泵转速相关。
本案例中,模型参数将通过分段线性估计方法得到,转速区间分为以下3个档:
- ω ≤ 900RPM
- 900 < ω ≤ 1500RPM
- ω > 1500RPM
正常情况下,水泵运行于由闭环控制器控制的0-3000 RPM参考转速区间内,该参考转速输入属于修正伪随机位序列信号。电机扭矩、泵扭矩、泵转速和压强数据在10 Hz的采样频率下采集
以下代码用于加载测量得到的这些信号并且画出参考转速和实际转速的图像:
load DynamicOperationData
figure
plot(t, RefSpeed, t, w)
xlabel('Time (s)')
ylabel('Pump Speed (RPM)')
legend('Reference','Actual')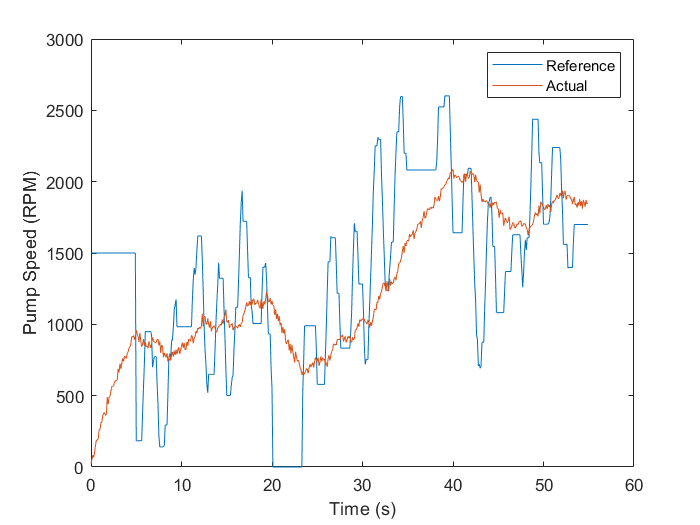
以下代码定义泵转速划分的三种区间范围:
第二步:模型识别
静态泵模型识别
使用泵转速ω(t)和压差Δp(t)作为静态泵模型方程的输入输出得到模型参数θ1和θ2的估计值,此处函数staticPumpEst用来执行估计过程:
th1 = zeros(3,1);
th2 = zeros(3,1);
dpest = nan(size(dp)); % 估计得到的压力差
[th1(1), th2(1), dpest(I1)] = staticPumpEst(w, dp, I1); % 转速区间为1时的Theta1, Theta2估计
[th1(2), th2(2), dpest(I2)] = staticPumpEst(w, dp, I2); % 转速区间为2时的Theta1, Theta2估计
[th1(3), th2(3), dpest(I3)] = staticPumpEst(w, dp, I3); % 转速区间为3时的Theta1, Theta2估计
plot(t, dp, t, dpest) % 比较压差测量值和估计值
xlabel('Time (s)')
ylabel('\Delta P')
legend('Measured','Estimated','Location','best')
title('Static Pump Model Validation')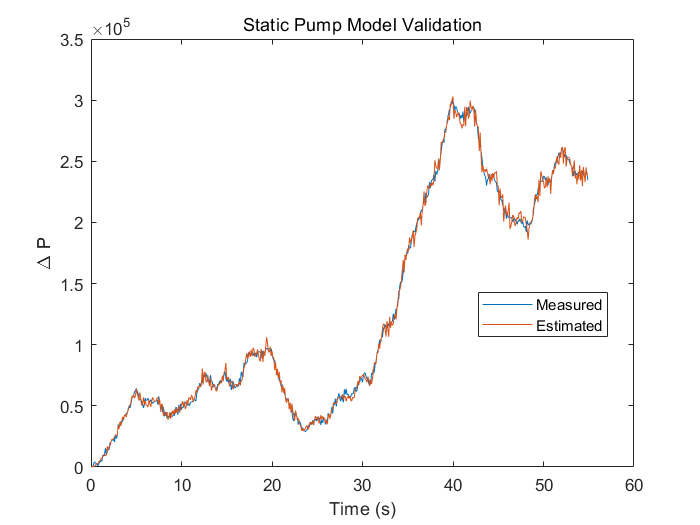
动态管道模型识别
类似于静态泵模型参数估计中的做法,给定方程$\hat{Q}(t)=\theta_3+\theta_4\sqrt{\Delta p(t)}+\theta_5\hat Q(t-1)$,通过使用流出率Q(t)和压差Δp(t)的测量值作为方程的输入输出,可以估计得到参数θ3,θ4,θ5的估计值。此处函数dynamicPipeEst用来执行方程估计过程:
function [x3, x4, x5, Qest] = dynamicPipeEst(dp, Q, I)
% 该方法用来估计动态管道方程(根据方程用矩阵形式反算参数)在不同泵转速设定下的方程参数
% I: 转速区间设定的索引
Q = Q(I);
dp = dp(I);
R1 = [0; Q(1:end-1)];
R2 = dp; R2(R2<0) = 0; R2 = sqrt(R2);
R = [ones(size(R2)), R2, R1];
% 移除未运行在定义区间内的样本
ii = find(I);
j = find(diff(ii)~=1);
R = R(2:end,:); R(j,:) = [];
y = Q(2:end); y(j) = [];
x = R\y;
x3 = x(1);
x4 = x(2);
x5 = x(3);
Qest = R*x;
endth3 = zeros(3,1);
th4 = zeros(3,1);
th5 = zeros(3,1);
[th3(1), th4(1), th5(1)] = dynamicPipeEst(dp, Q, I1); % 转速为区间为1时,估计Theta3, Theta4, Theta5
[th3(2), th4(2), th5(2)] = dynamicPipeEst(dp, Q, I2); % 转速为区间为2时,估计Theta3, Theta4, Theta5
[th3(3), th4(3), th5(3)] = dynamicPipeEst(dp, Q, I3); % 转速为区间为3时,估计Theta3, Theta4, Theta5不同于静态泵模型,动态管道模型具有对液体流出率动态依赖的关系。为了模拟该模型在不同转速区间下的表现,从控制系统工具箱中的LPV System模块开发得到一个分段线性模型。该模型被命名为LPV_pump_pipe,函数simulatePumpPipeModel用来运行该模拟过程:
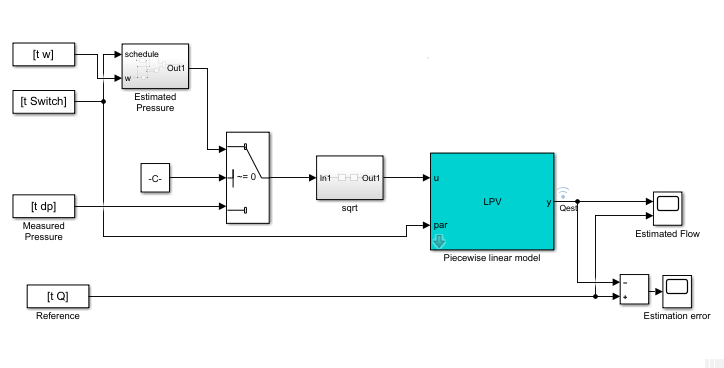
function Qest = simulatePumpPipeModel(Ts,th3,th4,th5)
% 动态管道系统的分段线性模型
% Ts: 采样时间
% w: 水泵转速
% th1, th2, th3 对于三种转速区间估计得到的参数,每个参数形状为3*1.
% 本函数要求安装控制系统工具箱.
ss1 = ss(th5(1),th4(1),th5(1),th4(1),Ts);
ss2 = ss(th5(2),th4(2),th5(2),th4(2),Ts);
ss3 = ss(th5(3),th4(3),th5(3),th4(3),Ts);
offset = permute([th3(1),th3(2),th3(3)]',[3 2 1]);
OP = struct('Region',[1 2 3]');
sys = cat(3,ss1,ss2,ss3);
sys.SamplingGrid = OP;
assignin('base','sys',sys)
assignin('base','offset',offset)
mdl = 'LPV_pump_pipe';
sim(mdl);
Qest = logsout.get('Qest');
Qest = Qest.Values;
Qest = Qest.Data;
end% 检查控制系统工具箱是否可用
ControlsToolboxAvailable = ~isempty(ver('control')) && license('test', 'Control_Toolbox');
if ControlsToolboxAvailable
% 模拟动态管道模型,使用压力测量值作为输入
Ts = t(2)-t(1);
Switch = ones(size(w));
Switch(I2) = 2;
Switch(I3) = 3;
UseEstimatedP = 0;
Qest_pipe = simulatePumpPipeModel(Ts,th3,th4,th5);
plot(t,Q,t,Qest_pipe) % 画出估计得到和测量得到液体流出率值
else
% 加载从分段线性simulink模型中预存的模拟结果
load DynamicOperationData Qest_pipe
Ts = t(2)-t(1);
plot(t,Q,t,Qest_pipe)
end
xlabel('Time (s)')
ylabel('Flow rate (Q), m^3/s')
legend('Measured','Estimated','Location','best')
title('Dynamic Pipe Model Validation')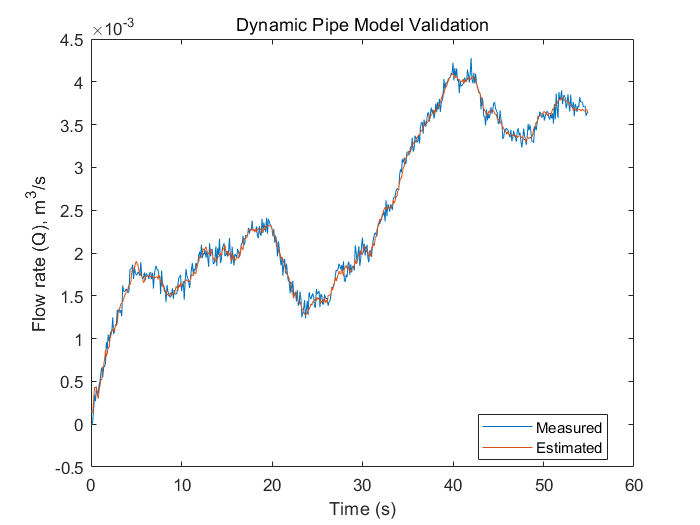
动态泵-管道模型识别
动态泵-管道模型使用同以上部分相同的参数(θ3,θ4,θ5),不同的是模型模拟使用静态泵模型中估计得到的压差,而不是测量得到的压差,其他步骤如同动态管道模型识别过程中的操作
if ControlsToolboxAvailable
UseEstimatedP = 1;
Qest_pump_pipe = simulatePumpPipeModel(Ts,th3,th4,th5);
plot(t,Q,t,Qest_pump_pipe) % 比较测量和预测得到的液体流出率
else
load DynamicOperationData Qest_pump_pipe
plot(t,Q,t,Qest_pump_pipe)
end
xlabel('Time (s)')
ylabel('Flow rate Q (m^3/s)')
legend('Measured','Estimated','location','best')
title('Dynamic Pump-Pipe Model Validation')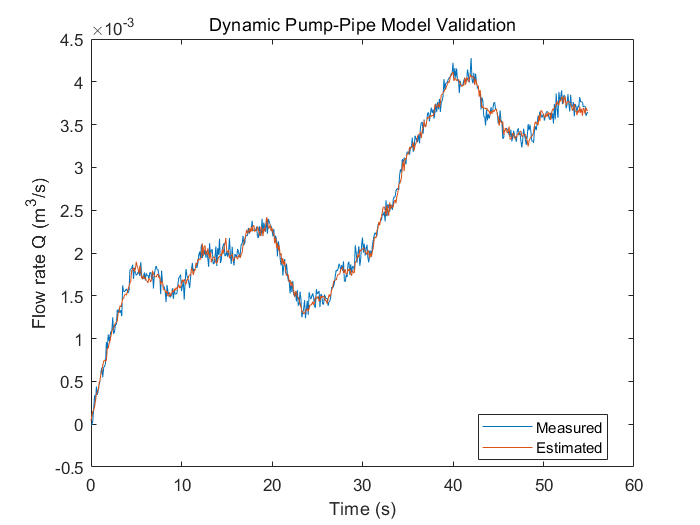
该结果与使用压差测量值得到的结果几乎一致(比较上图与上上图)
动态逆泵模型识别
参数θ6,…,θ10的估计符合同样的准则,回归分析测量得到的扭矩值,前一时刻的扭矩值以及速度值得到参数。然而,此时分速度区间分段线性模型并不能很好的拟合数据,因此使用了一种不同的黑盒方法。该方法使用有理回归器识别得到一个经数据拟合后的非线性的自回归各态历经模型identifyNonlinearARXModel,过程如下:
function syse = identifyNonlinearARXModel(Mmot,w,Q,Ts,N)
%identifyNonlinearARXModel 识别非线性的自回归各态历经模型对于双输入(w, Q), 单输出(Mmot)数据
% 输入:
% w: 转速
% Q: 液体流出率
% Mmot: 电机转矩
% N: 使用样本的个数
% 输出:
% syse: 识别到的模型
%
% 本函数使用来自系统识别工具箱中的NLARX估计器
sys = idnlarx([2 2 1 0 1],'','CustomRegressors',{'u1(t-2)^2','u1(t)*u2(t-2)','u2(t)^2'});
data = iddata(Mmot,[w Q],Ts);
opt = nlarxOptions;
opt.Focus = 'simulation';
opt.SearchOptions.MaxIterations = 500;
syse = nlarx(data(1:N),sys,opt);
end得到的非线性的自回归各态历经模型如下:
使用该模型模拟估计得到的电机扭矩值和测量得到的电机扭矩值绘图如下:
Mmot_est = sim(sys3,[w Q]);
plot(t,Mmot,t,Mmot_est) % 比较测量和估计得到的电机扭矩值
xlabel('Time (s)')
ylabel('Motor Torque (Nm)')
legend('Measured','Estimated','location','best')
title('Inverse pump model validation')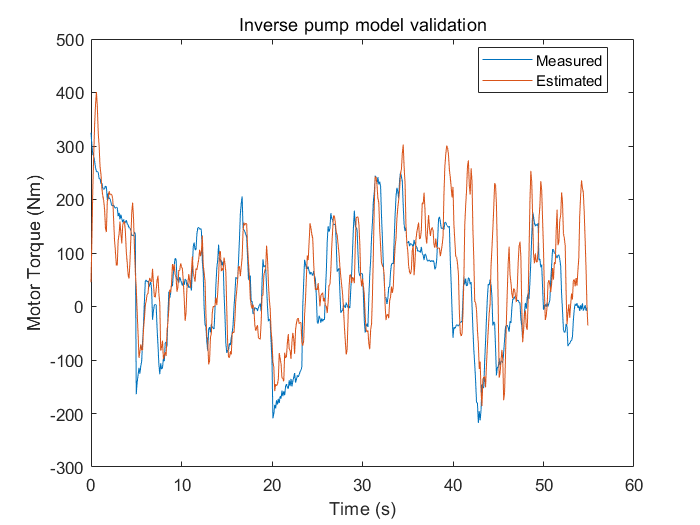
第三步:残差生成
由上述四种方法得到了四个模型的估计值,它们与对应测量值的差便可作为残差用作后续分析的输入
可视化得到的残差:
figure
subplot(221)
plot(t,r1)
ylabel('Static pump - r1')
subplot(222)
plot(t,r2)
ylabel('Dynamic pipe - r2')
subplot(223)
plot(t,r3)
ylabel('Dynamic pump-pipe - r3')
xlabel('Time (s)')
subplot(224)
plot(t,r4)
ylabel('Dynamic inverse pump - r4')
xlabel('Time (s)')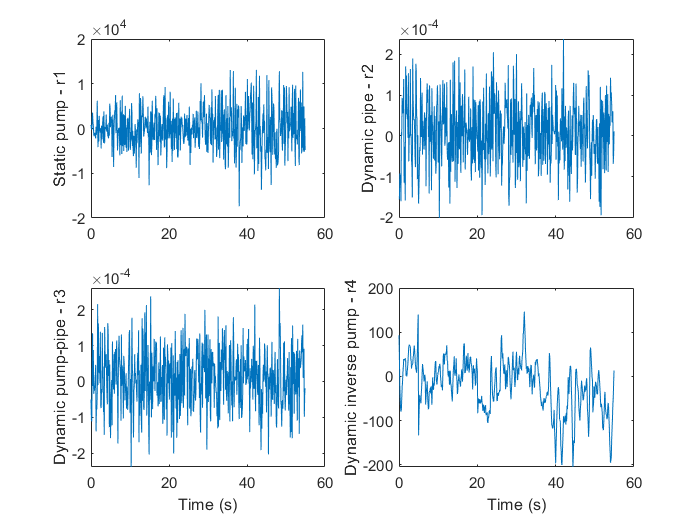
第四步:残差特征提取
从第三步中得到的残差,可以用来做特征提取(如常规的信号处理方法,最大峰值、信号方差等),得到的特征被用于故障类型分离
考虑对使用伪随机位序列作为输入,实现的一组50次实验的数据采集。每组实验分别按照以下10种模式进行:
- 健康水泵
- 故障1:间隙距磨损
- 故障2:叶轮出口小沉积
- 故障3:叶轮进口沉积
- 故障4:叶轮出口物理磨损
- 故障5:叶片折断
- 故障6:气穴现象
- 故障7:转速传感器偏差
- 故障8:流量计偏差
- 故障9:压力传感器偏差
下面加载实验数据(50 × 1 cell型数据):
load MultiSpeedOperationData
% 生成实验工况标签
Labels = {'Healthy','ClearanceGapWear','ImpellerOutletDeposit',...
'ImpellerInletDeposit','AbrasiveWear','BrokenBlade','Cavitation','SpeedSensorBias',...
'FlowmeterBias','PressureSensorBias'};接下来生成针对每种实验工况下每组数据得到的残差值,可使用以下helperComputeEnsembleResidues函数
function R = helperComputeEnsembleResidues(Ensemble,Ts,sys,x1,x2,x3,x4,x5)
%helperComputeEnsembleResidues Compute residues for a given dataset ensemble.
% This function is only in support of
% CentrifugalPumpFaultDiagnosisUsingResidualAnalysisExample. It may change
% in a future release.
% Copyright 2017 The MathWorks, Inc.
load_system('LPV_pump_pipe')
N = numel(Ensemble);
r1 = cell(N,1);
r2 = r1;
r3 = r1;
r4 = r1;
for kexp = 1:N
[r1{kexp},r2{kexp},r3{kexp},r4{kexp}] = ...
localComputeResidue(Ensemble{kexp},Ts,sys,x1,x2,x3,x4,x5);
end
R = [r1,r2,r3,r4];
%--------------------------------------------------------------------------
function [r1,r2,r3,r4] = localComputeResidue(Data,Ts,sys,x1,x2,x3,x4,x5)
% Residues for one dataset.
w = Data.Speed;
I1 = w<=900;
I2 = w>900 & w<=1500;
I3 = w>1500;
rho = 1800;
g = 9.81;
dp = Data.Head*rho*g;
Q = Data.Discharge;
Mmot = Data.MotorTorque;
dpest = NaN(size(dp));
dpest(I1) = [w(I1).^2 w(I1)]*[x1(1); x2(1)];
dpest(I2) = [w(I2).^2 w(I2)]*[x1(2); x2(2)];
dpest(I3) = [w(I3).^2 w(I3)]*[x1(3); x2(3)];
r1 = dp - dpest;
Switch = ones(size(w));
Switch(I2) = 2;
Switch(I3) = 3;
assignin('base', 'Switch', Switch);
assignin('base', 'UseEstimatedP', 0);
Qest_pipe = simulatePumpPipeModel(Ts,x3,x4,x5);
r2 = Q - Qest_pipe;
assignin('base', 'UseEstimatedP', 1);
Qest_pump_pipe = simulatePumpPipeModel(Ts,x3,x4,x5);
r3 = Q - Qest_pump_pipe;
zv = iddata(Mmot,[w Q/3600],Ts);
e = pe(sys,zv);
r4 = e.y;基于此函数的基础上,可以出10组实验得到的残差值,如健康水泵模型的残差计算如下所示:
因针对所有数据的计算较为耗时,这里直接导入计算后的结果,如下:
每组实验得到数据形式为50 × 4 cell型的残差数据,4表示共有4种残差值,对于每个cell中的元素,它们是形式为550 × 1时序数据
得到残差后,能有效区分故障类型的特征无法直观得到,因此使用函数helperGenerateFeatureTable生成多种常用的备选特征,诸如均值、最大峰值、方差、谷值、1-范数等,当然在此之前所有残差数据都应使用MinMaxScaler归一化到健康模式数据的范围内
function [T, MinMax] = helperGenerateFeatureTable(Ensemble, CandidateFeatures, Names, MinMax)
%helperGenerateFeatureTable Extract features from residues.
% This function is only in support of
% CentrifugalPumpFaultDiagnosisUsingResidualAnalysisExample. It may change
% in a future release.
% Copyright 2018 The MathWorks, Inc.
[N,m] = size(Ensemble); % 第N次实验,第m个残差
nf = length(Names); % nf个特征
F = zeros(N,m*nf);
ColNames = cell(1,m*nf);
for j = 1:nf
fcn = CandidateFeatures{j};
F(:,(j-1)*m+(1:m)) = cellfun(@(x)fcn(x),Ensemble,'uni',1);
ColNames((j-1)*m+(1:m)) = strseq(Names{j},1:m);
end
if nargout>1 && nargin<4
MinMax = [min(F); max(F)];
end
if nargin>3 || nargout>1
Range = diff(MinMax);
F = (F-MinMax(1,:))./Range;
end
T = array2table(F,'VariableNames',ColNames);CandidateFeatures = {@mean, @(x)max(abs(x)), @kurtosis, @var, @(x)sum(abs(x))};
FeatureNames = {'Mean','Max','Kurtosis','Variance','OneNorm'};
% 对于每种故障模式生成特征表
[HealthyFeature, MinMax] = helperGenerateFeatureTable(HealthyR, CandidateFeatures, FeatureNames);
Fault1Feature = helperGenerateFeatureTable(Fault1R, CandidateFeatures, FeatureNames, MinMax);
Fault2Feature = helperGenerateFeatureTable(Fault2R, CandidateFeatures, FeatureNames, MinMax);
Fault3Feature = helperGenerateFeatureTable(Fault3R, CandidateFeatures, FeatureNames, MinMax);
Fault4Feature = helperGenerateFeatureTable(Fault4R, CandidateFeatures, FeatureNames, MinMax);
Fault5Feature = helperGenerateFeatureTable(Fault5R, CandidateFeatures, FeatureNames, MinMax);
Fault6Feature = helperGenerateFeatureTable(Fault6R, CandidateFeatures, FeatureNames, MinMax);
Fault7Feature = helperGenerateFeatureTable(Fault7R, CandidateFeatures, FeatureNames, MinMax);
Fault8Feature = helperGenerateFeatureTable(Fault8R, CandidateFeatures, FeatureNames, MinMax);
Fault9Feature = helperGenerateFeatureTable(Fault9R, CandidateFeatures, FeatureNames, MinMax);每个残差特征表形式为50 × 20 table数据,20表示所有4种残差得到的特征(每种残差提取5种特征),50表示50次实验
下一步,将所有特征数据打上标签并拼接到一起,操作如下:
N = 50; % 每种实验的实验次数
FeatureTable = [...
[HealthyFeature(1:N,:), repmat(Labels(1),[N,1])];...
[Fault1Feature(1:N,:), repmat(Labels(2),[N,1])];...
[Fault2Feature(1:N,:), repmat(Labels(3),[N,1])];...
[Fault3Feature(1:N,:), repmat(Labels(4),[N,1])];...
[Fault4Feature(1:N,:), repmat(Labels(5),[N,1])];...
[Fault5Feature(1:N,:), repmat(Labels(6),[N,1])];...
[Fault6Feature(1:N,:), repmat(Labels(7),[N,1])];...
[Fault7Feature(1:N,:), repmat(Labels(8),[N,1])];...
[Fault8Feature(1:N,:), repmat(Labels(9),[N,1])];...
[Fault9Feature(1:N,:), repmat(Labels(10),[N,1])]];
FeatureTable.Properties.VariableNames{end} = 'Condition';
% 随机查看训练样本数据
disp(FeatureTable([2 13 37 49 61 62 73 85 102 120],:))第五步:分类器设计
使用散点绘图可视化模式分离
有了残差特征训练数据后,可以通过散点绘图目视的方法观察哪些特征适合用来分离故障。例如对于故障1:间隙距磨损,可以生成一幅标记上“Healthy”和“ClearanceGapWear”标签的特征散点图:

依稀可以看出,第1列和第17列的特征可以有效地分离健康和故障1工况
接下来仔细分析这两个特征:
f = figure;
Names = FeatureTable.Properties.VariableNames;
J = [1 17]; %查看第1列和第17列特征的名称
fprintf('Selected features for clearance gap fault: %s\n',strjoin(Names(J),', '))继续查看这两个特征构成的散点图:
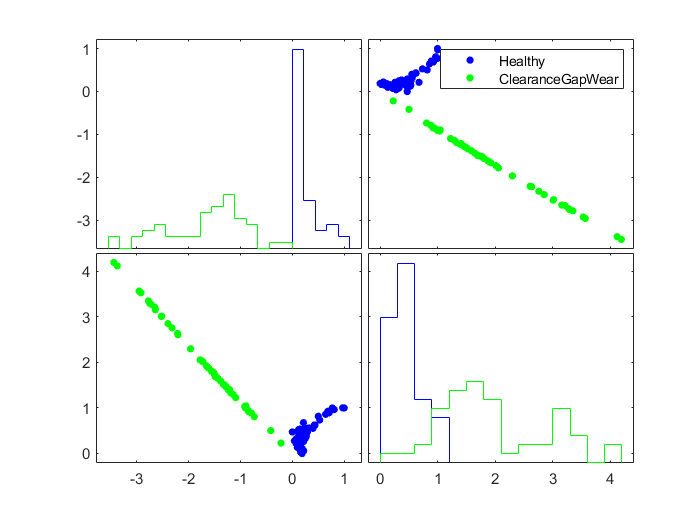
绘图显示,特征1:“Mean1”和特征17:“OneNorm1”可以被用来区分健康和间隙距故障工况,同样的分析方法可以应用于其他故障模式分析。对于所有的故障模式,都可以找到一组所有特征的子集特征来区分这些故障模式。然而,由于统一特征可能会被多种故障模式影响,所以故障分离会更加困难。例如特征1和特征17就并不是对所有故障类型都能区分,相反对于传感器偏差类故障来说,故障分离就简单一些,因为针对它们的诊断,有很多的有效特征可选
对于定义的三种传感器偏差类故障,可以从散点图的手动查看中选出合适的特征
figure;
I = strcmp(R,'Healthy') | strcmp(R,'PressureSensorBias') | strcmp(R,'SpeedSensorBias') | strcmp(R,'FlowmeterBias');
J = [1 4 6 16 20]; % 选择特征的索引,分别对应Mean1, Mean4, Max2, Variance4, OneNorm4五种特征
fprintf('Selected features for sensors'' bias: %s\n',strjoin(Names(J),', '))画出这五种特征在三种传感器偏差故障和健康时的散点图:
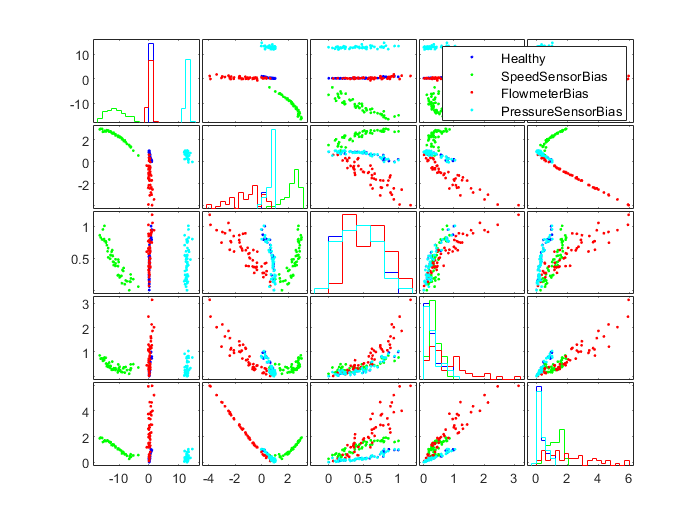
图中可以看出,这四种工况模式可以被单个或多个特征区分
接下来可以用选定的特征子集,训练一个含有20棵子树的装袋树分类器,来区分这几种传感器偏差故障
rng default % 保证再现性的随机种子
Mdl = TreeBagger(20, FeatureTable(I,[J 21]), 'Condition',...
'OOBPrediction','on',...
'OOBPredictorImportance','on');
figure
plot(oobError(Mdl))
xlabel('Number of trees')
ylabel('Misclassification probability')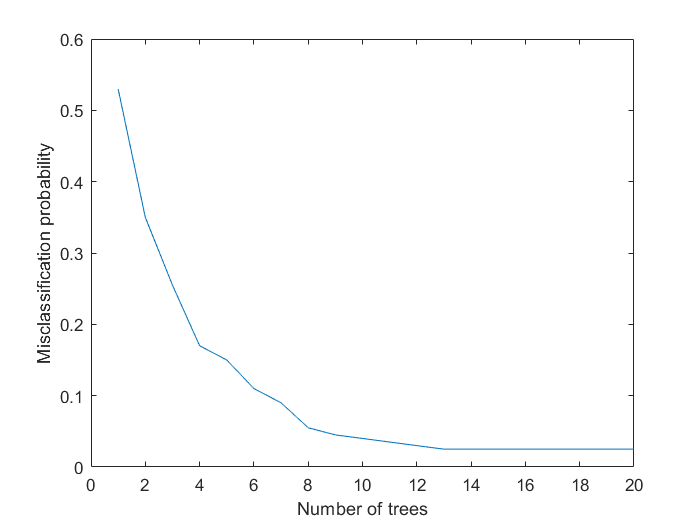
可以看出,最终错分率低于3%,证明可以选择一部分特征子集来区分故障子类(如归属于传感器偏差类的故障)
使用Classification Learner APP进行多分类
上述部分主要通过人工检测的方式选择特征划分故障类型,这种方法比较原始并且也不一定能覆盖所有的故障类型。一种更时髦的方法是使用Matlab统计和机器学习工具箱中的Classification Learner APP,以便快速建模和比较结果,操作过程如下:
导入数据并定义验证方式(此处选择20%样本留出)
训练并分析结果
从结果可看出,
- 三次支持向量机具有最好的分类效果,准确率达到了86%
- 间隙距磨损故障易和叶轮出口沉积故障的识别混淆
- 物理磨损易和叶片折断和健康状态两种模式混淆,推测可能是跟物理磨损的程度有关,轻微时更像健康状态,严重时更像叶片折断
要想导出生成的结果模型,可直接使用“导出”功能
第六步:总结
本案例介绍了基于比较测量数据和模型估计得到参数之间残差的方式建模分析离心泵故障的过程。当建模任务教复杂,且模型参数依赖于操作工况时,该方法是对参数估计和基于轨迹方法的很好补充
基于残差的故障诊断方法遵循以下步骤:
- 使用物理知识和黑盒系统识别技术对测量数据和系统输出的动态过程建模
- 计算测量信号和模型输出信号的残差,该残差在方差较大时可能需要经过平滑化、滤波处理
- 对每种残差提取残差特征,如峰值、功率、谷值等信号特征
- 选择可用特征,使用异常检测和分类技术进行故障检测
- 并不是所有残差和由它导出的特征都对每种故障的识别有效。对特征绘制散点图和柱状图有利于找到哪些特征对哪些特定的故障类型分离有用。对可被用来分离故障的特征挑选和评估过程属于可迭代过程(即可不断优化)