案例5：滚动轴承故障诊断

该案例展示了如何基于加速信号，尤其是有其他机械部件强掩蔽信号存在的情况下，进行故障分析诊断。该案例将演示如何使用包络谱分析和谱峰度来诊断轴承故障，同时也可被拓展到大数据应用方面

第一步：问题描述

滚动轴承的局部故障可能发生在外圈、内圈、保持架和滚动元件中。当健康滚动元件撞击内圈或外圈的局部故障，或故障滚动元件撞击健康内圈或外圈时，会激起高频谐振。下图中展示了健康滚动元件撞击轴承内圈局部故障。待研究的问题是如何检测并识别不同类型的故障。

第二步：数据描述

本案例数据来源于MFPT（Machinery Failure Prevention Technology）挑战数据，该数据包含了来自遭受不同故障类型的不同机械，它包括23组数据集。前20组数据情况如下（前20组数据集来自轴承试验台，后3组为实际采集的真实数据，分别来自油泵轴承、中速轴承和行星轴承，故障位置未知）：

  • 3组为健康状态
  • 3组为恒定载荷下的外圈故障
  • 7组为变载荷下的外圈故障
  • 7组为变载荷下的内圈故障

本案例分析过程中仅使用前20组带标签的数据

每组数据包含了一条时序加速信号“gs”，采样频率“sr”，轴转速“rate”，载荷“load”，以及代表不同故障位置的四种临界频率：外圈缺陷频率（BPFO），内圈缺陷频率（BPFI），轴承保持器损坏频率（FTF），轴承滚动件损坏频率（BSF）10。以下四个公式描述了这四种频率的计算：

  • $BPFD=\frac{nf_r}{2}(1-\frac d Dcos \phi)$
  • $BPFI=\frac{nf_r}{2}(1+\frac d Dcos \phi)$
  • $FTF=\frac{f_r}{2}(1-\frac d Dcos \phi)$
  • $BSF=\frac{D}{2d}[1-(\frac d D cos\phi)^2]$

公式中d为球直径，D为节径，变量fr为轴转速，n为滚动元件（滚珠）的个数，ϕ为轴承接触角

第三步：用于轴承诊断的包络谱分析

在MFPT数据中，轴转速都是恒定的，因此没有必要进行阶次跟踪作为预处理步骤以消除转速变化的影响

当健康滚动元件撞击故障内圈或外圈，或故障滚动元件撞击健康内圈或外圈时，所带来的冲击会调制出对应的临界频率如BFPO、BFPI、FTF、BSF等。因此幅度解调产生的包络信号，会传达出更多通过使用原始信号进行频谱分析无法得到的诊断信息。接下来以MFPT数据中的内圈故障数据为例：

可视化时域内原始内圈故障数据

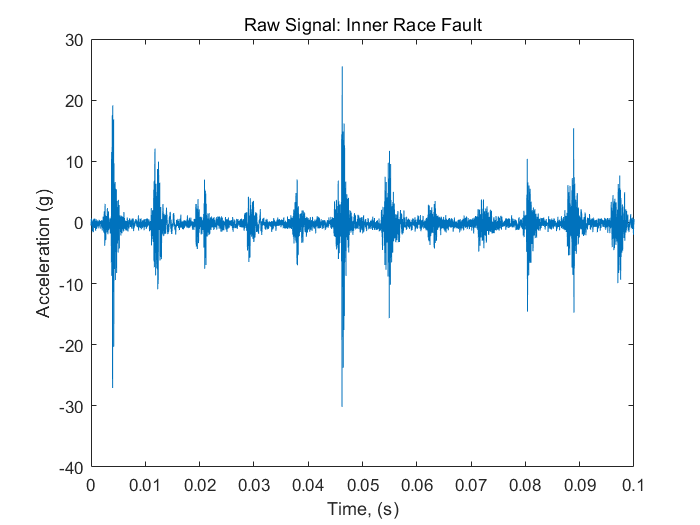
使用功率谱生成函数pspectrum查看频域内的原始数据

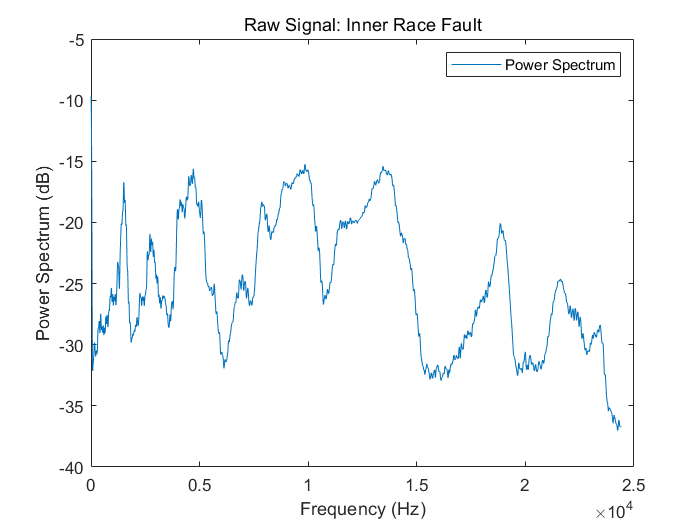
下面将频率放大到0-1000 Hz范围，进一步查看内圈缺陷频率的响应以及它出现第一次谐振时的情形

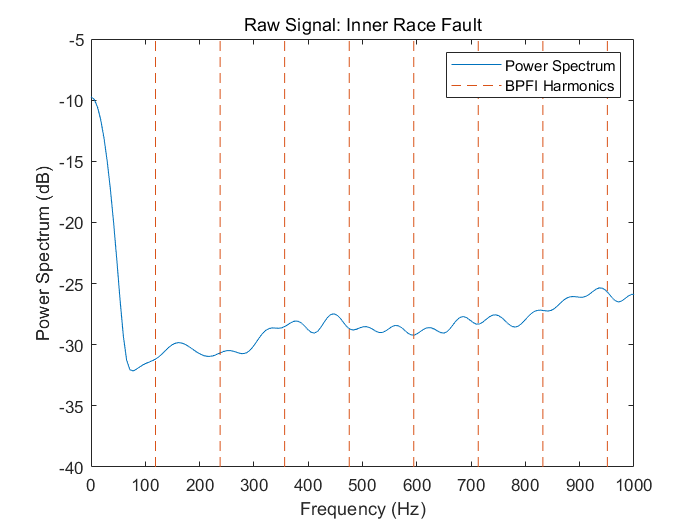
帮助函数helperPlotCombs如下：

从图中可以看到BPFI和它的谐波中观察不到明显的模式。此时对原始信号的频域分析也没法提供有用的诊断信息

再回过头来看时序数据，原始信号的振幅按一定频率调制，并且主频大约是1/0.009Hz ≈ 111Hz。已知健康滚动元件撞击内圈局部故障时的频率，也就是BPFI是118.875 Hz。这就说明该轴承可能有潜在的内圈故障

下面提取一段连续的振幅变化的时序数据进行可视化：

同时在下方使用函数envspectrum函数计算包络谱信息以提取调制振幅，并画出原始信号的包络

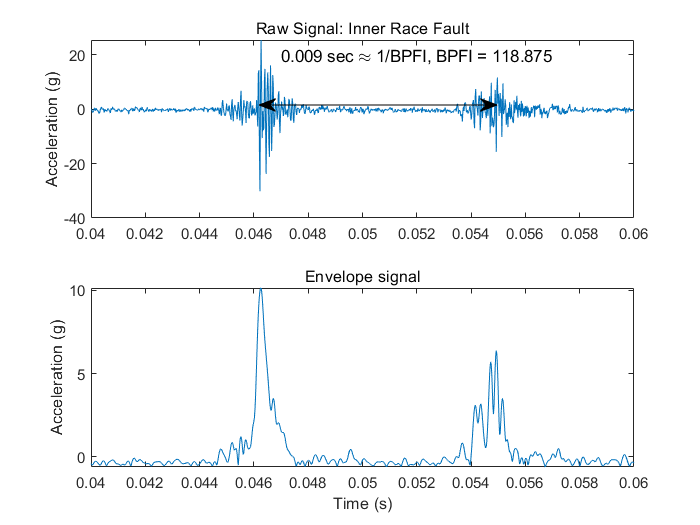
之后再使用包络信号计算功率谱，并查看对应的BPFI和它谐振的响应

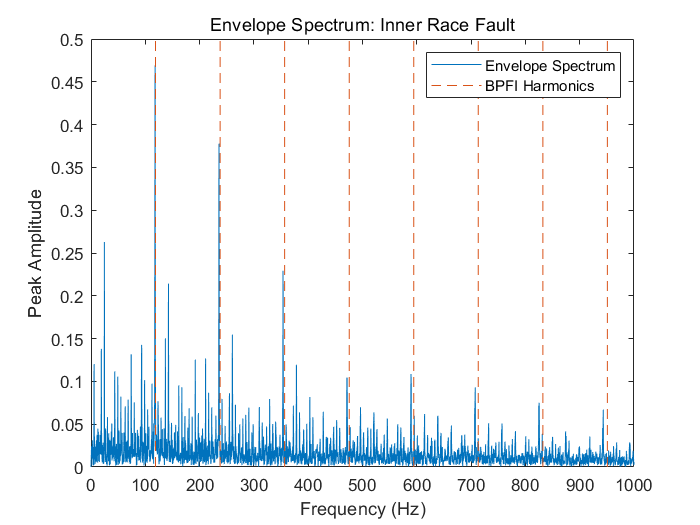
可以看出，大部分能量集中于BPFI和它的谐振上。这一现象指示了轴承内圈的故障，这也佐证了数据的故障标签

第四步：包络谱分析用于其他故障类型

现在将同样的包络谱分析方法应用于正常数据和轴承外圈故障数据中

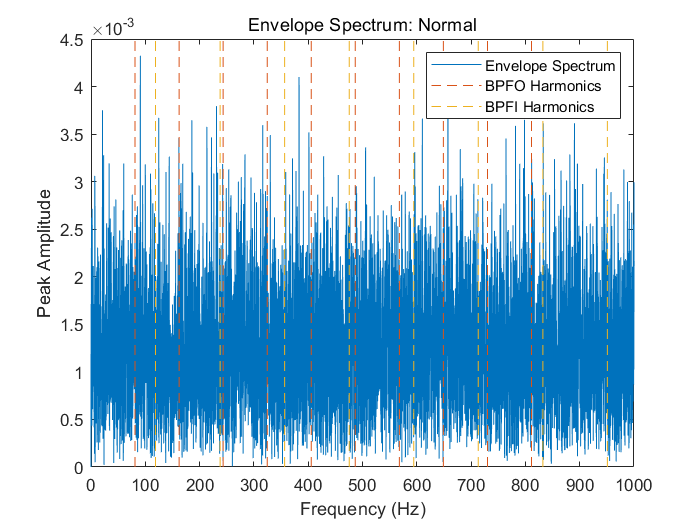
可以看出，对正常数据而言，包络谱并未表现出在BPFO和BPFI谐振上有明显的峰值出现

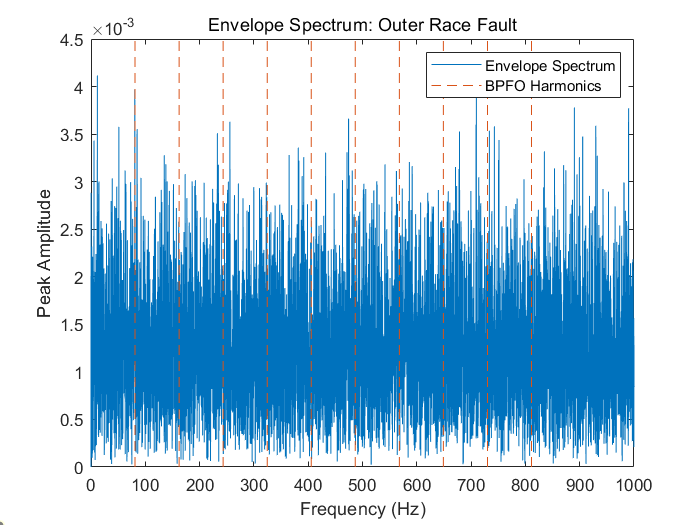
从外圈故障数据的包络谱来看，也没有明显的BPFO谐波出现。那么就可以断定包络谱无法区分外圈故障和健康状态吗？对此问题，可以退一步回过头来看不同条件下的原始时域数据

首先再次可视化这些时域数据并计算它们的峰度。峰度是随机变量的第四个标准化矩，它表征了信号的脉冲或随机变量尾部的肥瘦程度

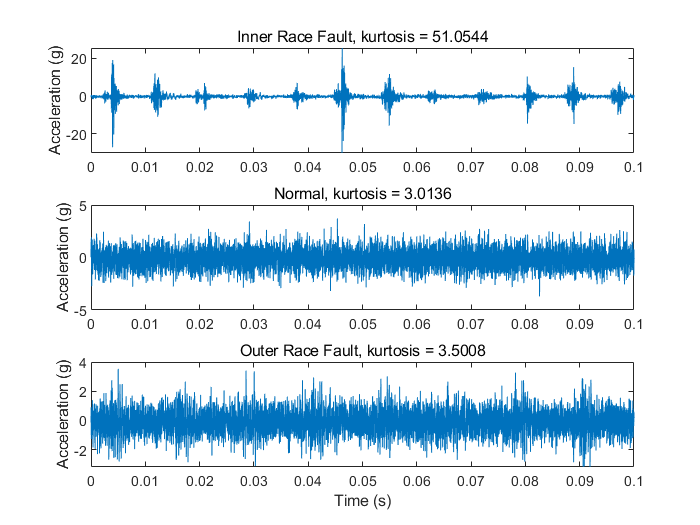
从上图可以看出，内圈故障数据有更大的峰度（即信号脉冲变化），这使得包络谱分析对它更有效。但是对于外圈故障而言，仅仅能看出轻微的BPFO谐波幅值重合，因为噪声较严重。对正常数据来说，甚至没有丝毫的幅值调制现象可以被观察到。所以综上，提取带有在BPFO处振幅调制的脉冲信号（或提高信噪比），在包络谱分析前属于关键的预处理步骤。下一节将介绍使用峰度图和谱峭度提取有着最高峰度值的信号，同时将包络谱分析方法应用在滤出的信号中

第五步：峰图和谱峰度用于波段选择

峰度图和谱峭度计算一定频率范围内的局部峰度。它们是找到拥有最高峰度（或最高信噪比）频率带信号的强力工具。在找到拥有最高峰度的频率带后，可以将带通滤波方法应用于原始信号来获得对包络谱分析更有帮助的强冲击信号

第六步：批处理

接下来，将该算法应用于批量训练数据中，该数据以文件集成数据的形式存储

工具箱中提供了有限的数据集，可将该数据集复制到当前文件夹下并开启写权限：

要想获得完整的数据集，可以使用本链接https://github.com/mathworks/RollingElementBearingFaultDiagnosis-Data来下载整个数据存储的压缩文件，可以用以下命令解压缩文件（压缩数据文件应位于当前程序位置）：

本案例中的结果从完整的数据集中得到。完整数据集包括14个mat文件组成的训练数据集（2个正常数据集，4个内圈故障数据集，7个外圈故障数据集）以及6个mat文件组成的测试数据集（1个正常数据集，2个内圈故障数据集，3个外圈故障数据集）

通过将函数句柄分配给ReadFcn以及WriteToMemberFcn，文件集成数据能导航到文件中，并以所需的格式检索数据。例如，MFPT数据是一个struct数据，存有振动信号gs，采样率sr等等。通过写入到readMFPTBearing函数中，而不是返回一个struct数据本身，可以使得文件集成数据可以直接返回振动信号gs，而不是struct结构数据

之后将其组合成tall数据类型：

从上一节的分析看出，带通滤波后的包络谱在BPFO和BPFI幅值位置时，是用来指示轴承故障的指示器。因此，下一步可以提取从所有训练数据中提取这两个健康指示量。为了使算法结果具有更好的鲁棒性，可以在BPFO和BPFI附近设置窄频带（带宽=10Δf，Δf表示功率谱的频率分辨率），然后找到窄频带中的最大幅值。这一算法被写进了以下bearingFeatureExtraction函数中。在之后的讨论中，包络谱在BPFO和BPFI附近的幅值分别被叫做“BPFOAmplitude”和“BPFIAmplitude”

一旦新的状态指示量被添加到文件集成数据中，可以指定SelectVariables来从文件集成数据存储中读取相关数据，同时创建一个包含所提取状态指示量的特征表

查看特征表

之后画散点图可视化创建的特征表

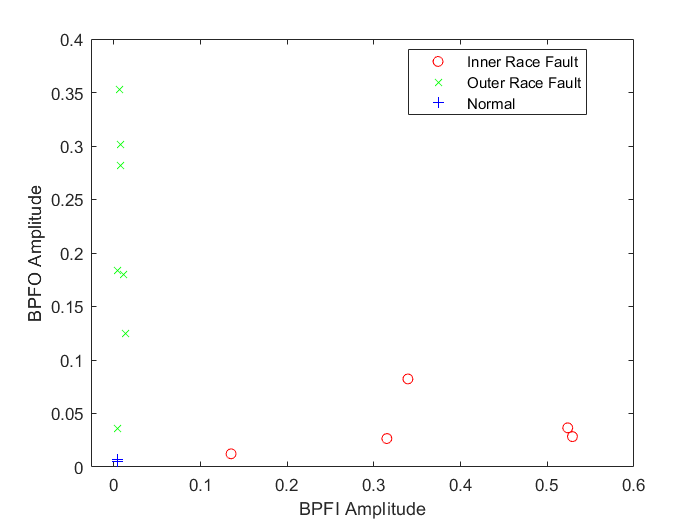
图中可以看到，BPFI和BPFO幅值的相对值可以作为判断不同故障类型的有效指标。因此，可以创造一个新的特征，即两个特征的对数比率，通过柱状图可画出不同故障类型时的该量的分布

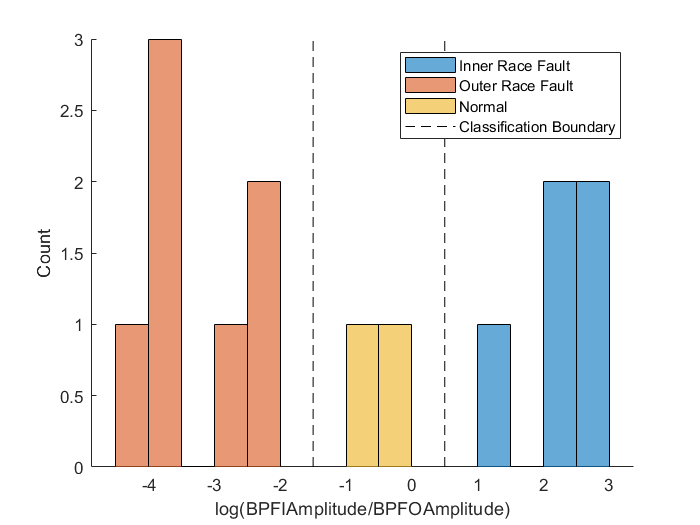
柱状图显示了明显的划分三种轴承状态类型能力，因此BPFI和BPFO的对数比率是一个有效分类故障类型的特征。为了简化例子，简单的分类器可以通过图中虚线的绝对值确定，即对数值 ≤  − 1.5时判断为外圈故障， − 1.5<对数值 ≤ 0.5时判断为正常状态，对数值 ≥ 0.5时判断为内圈故障

第七步：测试数据评估

现在，可对测试数据使用上述完整的工作流并评估上一部分中得到的分类器。以下测试数据包含1条正常数据集，2条内圈故障数据集，3条外圈故障数据集

设置变量名并提取特征

将所有测试数据生成tall数据并得到测试数据特征表

之后生成对数比率特征值并画出其柱状分布图

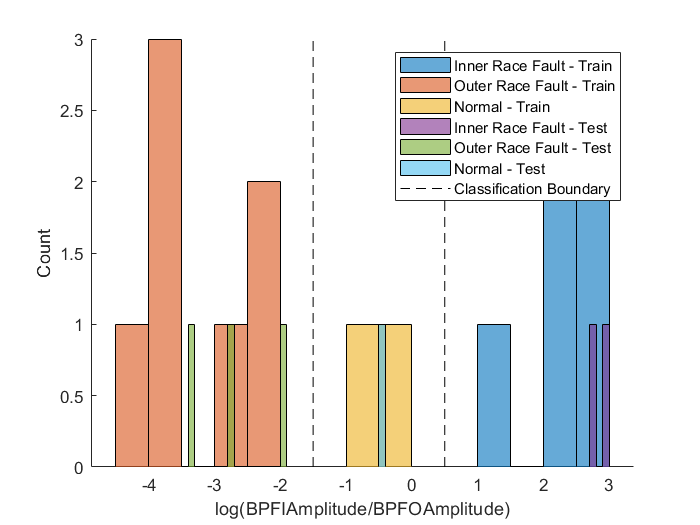
测试数据中BPFI和BPFO幅值计算得到的对数比率特征分布几乎同训练数据得到的该分布一致。说明上一节得到的这种简单的分类器在测试数据中可以实现完美分类。

当然需要注意的是，通常情况下单个特征不足以得到一个泛化能力好的分类器。更复杂的分类器可以通过将数据分割成多个块（创造更多的数据点），提取多个诊断相关的特征，然后根据它们的重要性排名选取一部分特征子集，最后使用机器学习工具箱中的Classification Learner APP训练模型来获得。案例6展示了这一工作流程的更多细节

第八步：总结

本案例展示了如何使用峰度图、谱峭度和包络谱识别滚动轴承中不同的故障类型。然后将算法应用于批量数据集，这一过程显示了在BPFI和BPFO处带通滤波后的幅值，是两个应用于轴承诊断时重要的状态指示量

参考：https://ww2.mathworks.cn/help/predmaint/ug/Rolling-Element-Bearing-Fault-Diagnosis.html